
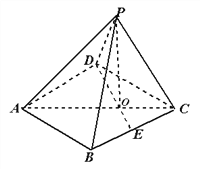
【题目】如图,已知四棱锥![]() 的底面的菱形,
的底面的菱形, ![]() ,点E是BC边的中点,AC和DE交于点O,PO
,点E是BC边的中点,AC和DE交于点O,PO ![]() ;
;
(1)求证: ![]() ;
;
(2)![]() 求二面角P-AD-C的大小。
求二面角P-AD-C的大小。
(3)在(2)的条件下,求异面直线PB与DE所成角的余弦值。
【答案】(1)见解析;(2)二面角![]() 的大小为
的大小为![]() ;(3)异面直线
;(3)异面直线![]() 、
、![]() 所成角的余弦值为
所成角的余弦值为![]() 。
。
【解析】试题分析:
(1)由题意可证得![]() ,结合射影定理可证得
,结合射影定理可证得![]() ;
;
(2)由题意找到二面角的平面角,结合三角函数值可得二面角![]() 的大小为
的大小为![]() .
.
(3)利用平移法结合余弦定理可得异面直线![]() 、
、![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
试题解析:
(1)在菱形![]() 中,连接
中,连接![]() 则
则![]() 是等边三角形。
是等边三角形。
![]() 点
点![]() 是边
是边![]() 的中点
的中点
![]()
![]() 平面
平面![]()
![]() 是斜线
是斜线![]() 在底面
在底面![]() 内的射影
内的射影
![]()
(2)![]()
菱形![]() 中,
中, ![]()
![]()
又![]() 平面
平面![]() ,
, ![]() 是
是![]() 在平面
在平面![]() 内的射影
内的射影
![]()
![]() 为二面角
为二面角![]() 的平面角
的平面角
在菱形![]() 中,
中, ![]() ,由(1)知,
,由(1)知, ![]() 等边三角形
等边三角形
![]() 点
点![]() 是
是![]() 边的中点,
边的中点, ![]() 与
与![]() 互相平分
互相平分
![]() 点
点![]() 是
是![]() 的重心
的重心
![]()
又![]() 在等边三角形
在等边三角形![]() 中,
中,
![]()
![]()
![]()
所以在![]() 中,
中, ![]()
![]()
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
(3)取![]() 中点
中点![]() ,连结
,连结![]() ,
, ![]()
则![]()
![]() 与
与![]() 所成角
所成角![]() 与
与![]() 所成角
所成角
连结![]()
![]() 平面
平面![]() ,
, ![]() 、
、![]() 平面
平面![]()
![]()
在![]() 中,
中, ![]()
![]()
在![]() 中,
中, ![]()
在![]() 中,
中, ![]()
由(2)可知, ![]()
设![]() 与
与![]() 所成的角为
所成的角为![]()
则![]()
所以异面直线![]() 、
、![]() 所成角的余弦值为
所成角的余弦值为![]()


科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() 判断
判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
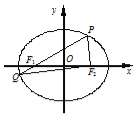
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设
(a>b>0)的左、右焦点分别为F1,F2,P为椭圆上一点(在x轴上方),连结PF1并延长交椭圆于另一点Q,设![]() =λ
=λ![]() .
.
(1)若点P的坐标为(1,![]() ),且△PQF2的周长为8,求椭圆C的方程;
),且△PQF2的周长为8,求椭圆C的方程;
(2)若PF2垂直于x轴,且椭圆C的离心率e∈[![]() ,
,![]() ],求实数λ的取值范围.
],求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
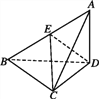
(1)求证:平面ABC⊥平面ACD;
(2)若E为AB中点,求点A到平面CED的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在D上的函数,若对D中的任意两数
是定义在D上的函数,若对D中的任意两数![]() ),恒有
),恒有![]() ,则称
,则称![]() 为定义在D上的C函数.
为定义在D上的C函数.
(1)试判断函数![]() 是否为定义域上的C函数,并说明理由;
是否为定义域上的C函数,并说明理由;
(2)若函数![]() 是R上的奇函数,试证明
是R上的奇函数,试证明![]() 不是R上的C函数;
不是R上的C函数;
(3)设![]() 是定义在D上的函数,若对任何实数
是定义在D上的函数,若对任何实数![]() 以及D中的任意两数
以及D中的任意两数![]() ),恒有
),恒有![]() ,则称
,则称![]() 为定义在D上的π函数. 已知
为定义在D上的π函数. 已知![]() 是R上的π函数,m是给定的正整数,设
是R上的π函数,m是给定的正整数,设![]() ,且
,且![]() ,记
,记![]() . 对于满足条件的任意函数
. 对于满足条件的任意函数![]() ,试求
,试求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() 上,
上, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]()
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设圆![]() 与点
与点![]() 的轨迹
的轨迹![]() 交于不同的四个点
交于不同的四个点![]() ,求四边形
,求四边形![]() 的面积的最大值及相应的四个点的坐标.
的面积的最大值及相应的四个点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(I)求棱锥C-ADE的体积;
(II)求证:平面ACE⊥平面CDE;
(III)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子里有编号为![]() 的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息, 你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球 C. 可能有5号球 D. 可能有6号球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com