
【题目】已知椭圆![]() 过点
过点![]() ,且焦距为4
,且焦距为4
(1)求椭圆![]() 的标准方程:
的标准方程:
(2)设![]() 为直线
为直线![]() 上一点,
上一点,![]() 为椭圆
为椭圆![]() 上一点.以
上一点.以![]() 为直径的圆恒过坐标原点
为直径的圆恒过坐标原点![]() .
.
(i)求![]() 的取值范围
的取值范围
(ii)是否存在圆心在原点的定圆恒与直线![]() 相切?若存在,求出该定圆的方程;若不存在,说明理由.
相切?若存在,求出该定圆的方程;若不存在,说明理由.
【答案】(1)![]() (2)(i)
(2)(i)![]() (ii)存在;定圆的方程
(ii)存在;定圆的方程![]()
【解析】
(1)将点![]() 代入椭圆方程,结合
代入椭圆方程,结合![]() 关系,即可求解;
关系,即可求解;
(2)(i)设![]() ,由已知有
,由已知有![]() ,可得
,可得![]() 代入椭圆方程,将
代入椭圆方程,将![]() 用
用![]() 表示,进而求出
表示,进而求出![]() 关于
关于![]() 的函数,根据函数特征求出最值;
的函数,根据函数特征求出最值;
(ii)将问题转化为原点到直线![]() 的距离是否为定值,先求出直线
的距离是否为定值,先求出直线![]() 方程,求出坐标原点到直线
方程,求出坐标原点到直线![]() 的距离,利用(i)中关系将
的距离,利用(i)中关系将![]() 用
用![]() 表示,整理即可得出结论.
表示,整理即可得出结论.
(1)将点的坐标代入椭圆![]() 的方程得
的方程得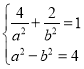 ,
,
解得![]() ,
,
所以椭圆C的方程为![]()
(2)设![]() .
.
因为以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,
,
所以![]() ,即
,即![]()
因为![]() 点在椭圆上,所以
点在椭圆上,所以![]() ;
;
(i)将![]() 代入椭圆,得
代入椭圆,得![]()
于是![]()
因为![]()
当且仅当![]() ,即
,即![]() 时,取等号.
时,取等号.
所以![]() 的取值范围为
的取值范围为![]()
(ii)存在.定圆的方程为![]() .
.
假设存在满足题意的定圆,则点![]() 到直线
到直线![]() 的距离为定值.
的距离为定值.
因为![]() ,所以直线
,所以直线![]() 方程为
方程为
![]() ,
,
整理可得![]()
所以![]() 到直线
到直线![]() 的距离
的距离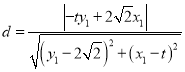
由(i)知,![]() ,得.
,得.![]()
![]() ,
,
注意到![]() ,知
,知![]()
所以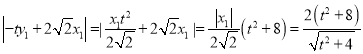
又![]()
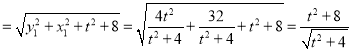 ,
,
所以,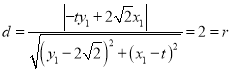
因此,直线![]() 与圆
与圆![]() 恒相切.
恒相切.


科目:高中数学 来源: 题型:
【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入![]() 种黄瓜的年收入
种黄瓜的年收入![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() .设甲大棚的投入为
.设甲大棚的投入为![]() (单位:万元),每年两个大棚的总收益为
(单位:万元),每年两个大棚的总收益为![]() (单位:万元)
(单位:万元)
(1)求![]() 的值;
的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使总收益![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为认真贯彻落实党中央国务院决策部署,坚持“房子是用来住的,不是用来炒的”定位,坚持调控政策的连续性和稳定性,进一步稳定某省市商品住房市场,该市人民政府办公厅出台了相关文件来控制房价,并取得了一定效果,下表是2019年2月至6月以来该市某城区的房价均值数据:
| 2 | 3 | 4 | 5 | 6 |
| 9.80 | 9.70 |
| 9.30 | 9.20 |
已知:![]() .
.![]()
(1)若变量![]() 、
、![]() 具有线性相关关系,求房价均价
具有线性相关关系,求房价均价![]() (千元/平方米)关于月份
(千元/平方米)关于月份![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测该市某城区7月份的房价.
(参考公式:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式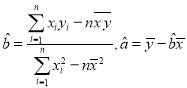 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角![]() 中,
中,![]() ,
,![]() 通过
通过![]() 以直线
以直线![]() 为轴顺时针旋转
为轴顺时针旋转![]() 得到(
得到(![]() ).点
).点![]() 为斜边
为斜边![]() 上一点.点
上一点.点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成的角取最大值时,求二面角
所成的角取最大值时,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,
,![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.当![]() 时,
时,![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
B.当![]() 时,
时,![]() 存在唯一极小值点
存在唯一极小值点![]() ,且
,且![]()
C.对任意![]() ,
,![]() 在
在![]() 上均存在零点
上均存在零点
D.存在![]() ,
,![]() 在
在![]() 上有且只有一个零点
上有且只有一个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水是生命之源,为了引导市民科学用水,我国加快阶梯水价推行,原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变,“建机制”是制定合理的阶梯用水价格某城市采用简单随机抽样的方法从郊区和城区分别抽取5户和20户居民的年人均用水量(单位:吨)进行调研,抽取数据的茎叶图如下:
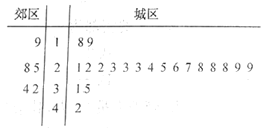
(1)若在郊区的这5户居民中随机抽取2户,求“被抽取的2户年人均用水量的和超过60吨”的概率;
(2)若该城市郊区和城区的居民户数比为1:5,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,只保证这一梯次的居民用户用水价格不变,试根据样本估计总体的思想分析此方案是否符合国家“保基本”政策.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从广安市某中学校的![]() 名男生中随机抽取
名男生中随机抽取![]() 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于![]() cm和
cm和![]() cm之间,将测量结果按如下方式分成八组:第一组
cm之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,...,第八组
,...,第八组![]() ,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为![]() 人.
人.
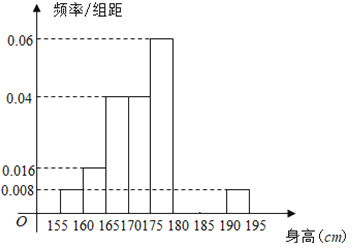
(1)求第七组的频率;
(2)估计该校![]() 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在![]() cm以上(含
cm以上(含![]() cm)的人数;
cm)的人数;
(3)若从样本中身高属于第六组和第八组的所有男生中随机抽取两名男生,求抽出的两名男生在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,椭圆的左,右焦点分别为F1,F2,点M为椭圆上的一个动点,△MF1F2面积的最大值为
,椭圆的左,右焦点分别为F1,F2,点M为椭圆上的一个动点,△MF1F2面积的最大值为![]() ,过椭圆外一点(m,0)(m>a)且倾斜角为
,过椭圆外一点(m,0)(m>a)且倾斜角为![]() 的直线l交椭圆于C,D两点.
的直线l交椭圆于C,D两点.
(1)求椭圆的方程;
(2)若![]() ,求m的值.
,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com