
已知函数![]()
(1)若1是关于x的方程![]() 的一个解,求t的值;
的一个解,求t的值;
(2)当![]() 时,解不等式
时,解不等式![]() ;
;
(3)若函数![]() 在区间
在区间![]() 上有零点,求t的取值范围.
上有零点,求t的取值范围.
解:(1) ∵1是方程f(x)-g(x)=0的解,∴loga2=loga(2+t)2,
∴(2+t)2=2 又∵t+2>0 ∴t+2=![]() ∴t=
∴t=![]() .
.
(2)∵t=-1时,loga(x+1)≤loga(2x-1)2 又∵0<a<1
∴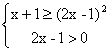 ∴
∴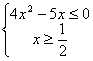 ∴
∴
∴解集为:{x|![]() }
}
(3)解法一:∵F(x)=tx2+x-2t+2
由F(x)=0得:t=![]() 且-1<x≤2)
且-1<x≤2)
∴t=![]()
设U=x+2 ( 1<U≤4且U≠2![]() )
)
则 t=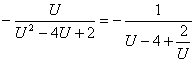
令![]() =
=![]() ∵
∵![]()
∴当![]() 时,
时,![]() 是减函数,
是减函数,
当![]() 时,
时,![]() 是增函数,
是增函数,
且![]() .
.
∴![]() 且
且![]() ≠4.
≠4.
∴![]() 4-
4-![]() <0或0<4-
<0或0<4-![]() ≤
≤![]() ,
,
t的取值范围为:![]() .
.
解法二:若t=0,则F(x)=x+2在![]() 上没有零点.
上没有零点.
下面就t≠0时分三种情况讨论:
① 方程F(x)=0在![]() 上有重根x1=x2,
上有重根x1=x2,
② 则Δ=0,解得:t=![]()
又x1=x2=![]() ∈
∈![]() ,∴t=
,∴t=![]() .
.
②F(x)在![]() 上只有一个零点,且不是方程的重根,则有F(-1)F(2)<0
上只有一个零点,且不是方程的重根,则有F(-1)F(2)<0
解得:t<-2或 t>1
又经检验:t=-2或t=1时,F(x)在![]() 上都有零点;
上都有零点;
∴t≤-2或 t≥1.
③ 方程F(x)=0在![]() 上有两个相异实根,则有:
上有两个相异实根,则有:
 解得:
解得:![]()
F(-1)>0 F(-1)<0
F(2)>0 F(2)<0
综合①②③可知:t的取值范围为![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x)+1 |
| f(x)-1 |
| 1 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| an |
| (y-1)2 |
| 4 |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a | 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市高三上学期期末模拟理科数学试卷(解析版) 题型:解答题
(本小题满分l2分)
已知函数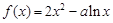
(1)若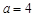 ,求函数
,求函数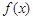 的极小值;
的极小值;
(2)设函数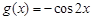 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量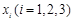 使得
使得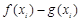 的值相等,若存在,请求出
的值相等,若存在,请求出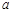 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com