Question

【题目】已知函数 ，数列{an}满足 ．
（1）求证：数列{ }是等差数列；
（2）求数列{an}的通项公式；
（3）记Sn=a1a2+a2a3+…+anan+1 ， 求Sn ．

Answer 1

【答案】
（1）证明：∵函数 ，数列{an}满足 ，

∴ ，

∴ =3+ ，

∴ =3， =1，

∴数列{ }是首项为1，公差为3的等差数列

（2）解：∵数列{ }是首项为1，公差为3的等差数列，

∴ =1+（n﹣1）×3=3n﹣2，

∴an= ．

（3）解：∵anan+1= = （ ），

∴Sn=a1a2+a2a3+…+anan+1

= （1﹣ + + +…+ ）

=

= ．

【解析】（1）由已知利用函数性质得 ，从而 =3+ ，由此能证明数列{ }是首项为1，公差为3的等差数列．（2）由 =1+（n﹣1）×3=3n﹣2，能求出an ． （3）anan+1= = （ ），利用裂项求和法能求出Sn ．
【考点精析】根据题目的已知条件，利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系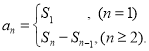；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．