
【题目】已知直线l1:mx﹣y=0,l2:x+my﹣m﹣2=0.
(1)求证:对m∈R,l1与l2的交点P在一个定圆上;
(2)若l1与定圆的另一个交点为P1 , l2与定圆的另一个交点为P2 , 求当m在实数范围内取值时,△PP1P2的面积的最大值及对应的m.
【答案】
(1)解:如图所示:l1:﹣y=0,过定点(0,0), ![]() =m;
=m;
l2:x+my﹣m﹣2=0,m(y﹣1)+x﹣2=0, ![]() =﹣
=﹣ ![]()
令y﹣1=0,x﹣2=0.得y=1,x=2,∴过定点(2,1),
∵ ![]()
![]() =﹣1,∴直线与直线互相垂直,
=﹣1,∴直线与直线互相垂直,
∴直线与直线的交点必在以(0,0),(2,1)为一条直径端点的圆上,且圆心(1, ![]() ),半径r=
),半径r= ![]()
![]() =
= ![]() ,
,
∴圆的方程为(x﹣1)2+(y﹣ ![]() )2=
)2= ![]() .
.
即x2+y2﹣2x﹣y=0;

(2)解:由(1)得:(0,0),(2,1).当P点在定圆上移动时,△PP1P2的底边P1P2为定值2r.当三角形的高最大时,△PP1P2的面积最大.
故三角形面积最大为 ![]() 2rr=
2rr= ![]()
又与圆的交点为P( ![]() ,
, ![]() ),且OP与P1P2的夹角是45°.
),且OP与P1P2的夹角是45°.
∴|OP|= ![]() =
= ![]() ,即
,即 ![]() +
+ ![]() =
= ![]() ,解得:m=3或m=
,解得:m=3或m= ![]()
故当m=3或m= ![]() 时,△PP1P2的面积取得最大值
时,△PP1P2的面积取得最大值 ![]() .
.
【析】(1)联立两条直线方程,消去m,即得到l1和l2的交点M的方程,判断对m∈R,l1与l2的交点P在一个定圆上;(2)由(1)得:(0,0),(2,1).当P点在定圆上移动时,△PP1P2的底边P1P2为定值2r.当三角形的高最大时,△PP1P2的面积最大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,数列{an}满足
,数列{an}满足 ![]() .
.
(1)求证:数列{ ![]() }是等差数列;
}是等差数列;
(2)求数列{an}的通项公式;
(3)记Sn=a1a2+a2a3+…+anan+1 , 求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校的平面示意图为如下图五边形区域![]() ,其中三角形区域
,其中三角形区域![]() 为生活区,四边形区域
为生活区,四边形区域![]() 为教学区,
为教学区, ![]() 为学校的主要道路(不考虑宽度).
为学校的主要道路(不考虑宽度). ![]() .
.
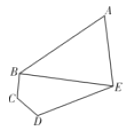
(1)求道路![]() 的长度;(2)求生活区
的长度;(2)求生活区![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:①f(0)=0,②f(x)+f(1﹣x)=1,③f( ![]() )=
)= ![]() f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(
f(x)且当0≤x1<x2≤1时,f(x1)≤f(x2),则f( ![]() )+f(
)+f( ![]() )等于( )
)等于( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,四个顶点构成的菱形的面积是4,圆
,四个顶点构成的菱形的面积是4,圆![]() 过椭圆
过椭圆![]() 的上顶点
的上顶点![]() 作圆
作圆![]() 的两条切线分别与椭圆
的两条切线分别与椭圆![]() 相交于
相交于![]() 两点(不同于点
两点(不同于点![]() ),直线
),直线![]() 的斜率分别为
的斜率分别为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 变化时,①求
变化时,①求![]() 的值;②试问直线
的值;②试问直线![]() 是否过某个定点?若是,求出该定点;若不是,请说明理由.
是否过某个定点?若是,求出该定点;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.经过空间内的三个点有且只有一个平面
B.如果直线l上有一个点不在平面α内,那么直线上所有点都不在平面α内
C.四棱锥的四个侧面可能都是直角三角形
D.用一个平面截棱锥,得到的几何体一定是一个棱锥和一个棱台
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求曲线![]() 的直角坐标方程,并指出其表示何种曲线;
的直角坐标方程,并指出其表示何种曲线;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,
,
试求当![]() 时,
时, ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com