
【题目】设函数![]() .若
.若![]() 在
在![]() 上的最大值为2,则实数a所有可能的取值组成的集合是________.
上的最大值为2,则实数a所有可能的取值组成的集合是________.
【答案】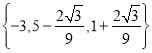
【解析】
根据函数的最大值,依据![]() 可求出
可求出![]() 的两种情况.讨论
的两种情况.讨论![]() 的不同取值,去掉内层的绝对值,利用导数分析三次函数的极值点,进而求得最大值与最小值.通过函数的上下平移,结合最值即可求得
的不同取值,去掉内层的绝对值,利用导数分析三次函数的极值点,进而求得最大值与最小值.通过函数的上下平移,结合最值即可求得![]() 的所有取值.
的所有取值.
因为函数![]() .若
.若![]() 在
在![]() 上的最大值为2
上的最大值为2
所以![]() ,即
,即![]()
当![]() 时,不等式化为
时,不等式化为![]() ,解得
,解得![]()
当![]() 时,不等式化为
时,不等式化为![]() ,解得
,解得![]()
由以上可知:
(1) 当![]() 时,函数解析式可化为
时,函数解析式可化为![]()
令![]() ,则
,则![]()
当![]() 时解得
时解得![]()
当![]() 时,
时, ![]() ,即
,即![]() 在
在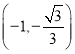 上单调递增
上单调递增
当![]() 时,
时, ![]() ,即
,即![]() 在
在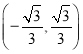 上单调递减
上单调递减
当![]() 时,
时, ![]() ,即
,即![]() 在
在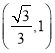 上单调递增.
上单调递增.
所以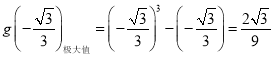 ,
,
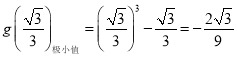
![]()
当![]() 时,
时, ![]() 向下平移
向下平移![]() 个单位可得
个单位可得![]() 的图像
的图像
因为![]() 在
在![]() 上的最大值为2
上的最大值为2
所以只需满足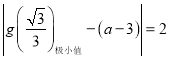 即可,即
即可,即![]() ,解得
,解得![]() ,或
,或![]() (舍)
(舍)
当![]() 时,
时, ![]() 向上平移
向上平移![]() 个单位可得到
个单位可得到![]() 的图像
的图像
由![]() 在
在![]() 上的最大值为2
上的最大值为2
可知只需满足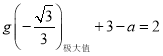 即可.即
即可.即![]() ,解得
,解得![]() ,符合题意
,符合题意
(2) 当![]() ,函数解析式可化为
,函数解析式可化为![]()
令![]() ,则
,则![]()
所以![]() 在
在![]() 上单调递增
上单调递增
则![]()
![]()
当![]() 时,
时,![]() 向下平移
向下平移![]() 个单位可得
个单位可得![]()
由![]() 在
在![]() 上的最大值为2
上的最大值为2
只需![]() ,即
,即![]() 解得
解得![]() 或
或![]() (舍)
(舍)
当![]() 时,
时, ![]() 向上平移
向上平移![]() 个单位可得
个单位可得![]()
由![]() 在
在![]() 上的最大值为2
上的最大值为2
只需![]() ,即
,即![]() 解得
解得![]() 或
或![]() (舍)
(舍)
综上可知,满足条件的所有可能的![]() 为
为![]()
![]() 和
和![]()
故答案为: 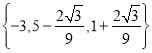


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】南北朝时,张邱建写了一部算经,即《张邱建算经》,在这本算经中,张邱建对等差数列的研究做出了一定的贡献.例如算经中有一道题为:“今有十等人,每等一人,宫赐金以等次差降之,上三人先入,得金四斤,持出,下四人后入得金三斤,持出,中间三人未到者,亦依等次更给”,则某一等人比其下一等人多得________斤金.(不作近似计算)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,直线l的参数方程为![]() (t为参数,
(t为参数,![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)当![]() 时,写出直线l的普通方程及曲线C的直角坐标方程;
时,写出直线l的普通方程及曲线C的直角坐标方程;
(2)已知点![]() ,设直线l与曲线C交于A,B两点,试确定
,设直线l与曲线C交于A,B两点,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面为矩形,且AB=![]() ,BC=1,E,F分别为AB,PC中点.
,BC=1,E,F分别为AB,PC中点.

(1)求证:EF∥平面PAD;
(2)若平面PAC⊥平面ABCD,求证:平面PAC⊥平面PDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据幼儿身心发展的特征,幼儿园通常着重在健康、科学、社会、语言、艺术五大领域对幼儿展开全方位的教育和培养.经调查发现,一个幼儿除了在幼儿园进行五大领域的系统学习之外,还会报一些课外兴趣班.而家长朋友们对于是否额外报这些课外兴趣班的态度也是不一样的.某调查机构对某幼儿园的100名幼儿家长就孩子是否报课外兴趣班的赞同程度进行调查统计,得到家长对幼儿报课外兴趣班赞同度![]() 的频数分布表:
的频数分布表:
赞同度 |
|
|
|
|
|
家长数 | 2 | 12 | 14 | 28 | 44 |
(1)分别计算对幼儿报兴趣班的赞同度不低于![]() 的家长比例和对幼儿报兴趣班的赞同度低于
的家长比例和对幼儿报兴趣班的赞同度低于![]() 的家长比例;
的家长比例;
(2)求家长对幼儿报兴趣班的赞同度的平均数与方差的估计值.(同一组中的数据用该组区间的中点值代替)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com