
【题目】给出下列命题:
①直线l的方向向量为 ![]() =(1,﹣1,2),直线m的方向向量
=(1,﹣1,2),直线m的方向向量 ![]() =(2,1,﹣
=(2,1,﹣ ![]() ),则l与m垂直;
),则l与m垂直;
②直线l的方向向量 ![]() =(0,1,﹣1),平面α的法向量
=(0,1,﹣1),平面α的法向量 ![]() =(1,﹣1,﹣1),则l⊥α;
=(1,﹣1,﹣1),则l⊥α;
③平面α、β的法向量分别为 ![]() =(0,1,3),
=(0,1,3), ![]() =(1,0,2),则α∥β;
=(1,0,2),则α∥β;
④平面α经过三点A(1,0,﹣1),B(0,1,0),C(﹣1,2,0),向量 ![]() =(1,u,t)是平面α的法向量,则u+t=1.
=(1,u,t)是平面α的法向量,则u+t=1.
其中真命题的是 . (把你认为正确命题的序号都填上)
【答案】①④
【解析】解:对于①,∵ ![]() =(1,﹣1,2),
=(1,﹣1,2), ![]() =(2,1,﹣
=(2,1,﹣ ![]() ),∴
),∴ ![]()
![]() =1×2﹣1×1+2×(﹣
=1×2﹣1×1+2×(﹣ ![]() )=0,
)=0,
∴ ![]() ⊥
⊥ ![]() ,
,
∴直线l与m垂直,①正确;
对于②, ![]() =(0,1,﹣1),
=(0,1,﹣1), ![]() =(1,﹣1,﹣1),
=(1,﹣1,﹣1),
∴ ![]()
![]() =0×1+1×(﹣1)+(﹣1)×(﹣1)=0,
=0×1+1×(﹣1)+(﹣1)×(﹣1)=0,
∴ ![]() ⊥
⊥ ![]() ,∴l∥α或lα,②错误;
,∴l∥α或lα,②错误;
对于③,∵ ![]() =(0,1,3),
=(0,1,3), ![]() =(1,0,2),
=(1,0,2),
∴ ![]() 与
与 ![]() 不共线,
不共线,
∴α∥β不成立,③错误;
对于④,∵点A(1,0,﹣1),B(0,1,0),C(﹣1,2,0),
∴ ![]() =(﹣1,1,1),
=(﹣1,1,1), ![]() =(﹣1,1,0),
=(﹣1,1,0),
向量 ![]() =(1,u,t)是平面α的法向量,
=(1,u,t)是平面α的法向量,
∴ 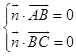 ,
,
即 ![]() ;
;
则u+t=1,④正确.
综上,以上真命题的序号是①④.
所以答案是:①④.
【考点精析】关于本题考查的平面的法向量,需要了解若向量![]() 所在直线垂直于平面
所在直线垂直于平面![]() ,则称这向量垂直于平面
,则称这向量垂直于平面![]() ,记作
,记作![]() ,如果
,如果![]() ,那么向量
,那么向量![]() 叫做平面
叫做平面![]() 的法向量才能得出正确答案.
的法向量才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,直线AB经过☉O上的点C,并且OA=OB,CA=CB,☉O交直线OB于E,D两点,连接EC,CD. 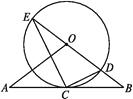
(1)求证:直线AB是☉O的切线;
(2)若tan∠CED= ![]() ,☉O的半径为3,求OA的长.
,☉O的半径为3,求OA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱长为a的正方体ABCD﹣A1B1C1D1中,点M,N,E分别是棱A1B1 , A1D1 , C1D1的中点. 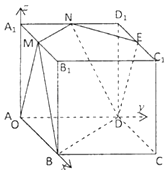
(1)过AM作一平面,使其与平面END平行(只写作法,不需要证明);
(2)在如图的空间直角坐标系中,求直线AM与平面BMND所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+4
(1)若f(x)为偶函数,求b的值;
(2)若f(x)有零点,求b的取值范围;
(3)求f(x)在区间[﹣1,1]上的最大值g(b).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中实数
,其中实数![]() 为常数,
为常数,![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(3)当![]() 时,如果函数
时,如果函数![]() 不存在极值点,求
不存在极值点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD所在的平面和平面![]() 互相垂直,等腰梯形
互相垂直,等腰梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点,
的中点, ![]() 为底面
为底面![]() 的重心.
的重心.
(Ⅰ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A=B=R,x∈A,y∈B,f:x→y=ax+b是从A到B的映射,若1和8的原象分别是3和10,则5在f下的象是( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为实常数.
为实常数.
(1)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,直线
时,直线![]() 、
、![]() 与函数
与函数![]() 的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.求证:
的图象一共有四个不同的交点,且以此四点为顶点的四边形恰为平行四边形.求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com