
【题目】f(x)=(ax2+x﹣1)ex
(1)当a<0时,求f(x)的单调区间;
(2)若a=﹣1,f(x)的图象与g(x)= ![]() x3+
x3+ ![]() x2+m的图象有3个不同的交点,求实数m的范围.
x2+m的图象有3个不同的交点,求实数m的范围.
【答案】
(1)解:∵f'(x)=ex(ax2+x+1+2ax+1)=axex(x+ ![]() ),且a<0,
),且a<0,
∴当a∈(﹣ ![]() ,0)时,f(x)在(﹣∞,0)上是减函数,在(0,﹣
,0)时,f(x)在(﹣∞,0)上是减函数,在(0,﹣ ![]() )上是增函数,在(﹣
)上是增函数,在(﹣ ![]() ,+∞)上是减函数,
,+∞)上是减函数,
当a=﹣ ![]() 时,f(x)在(﹣∞,+∞)上单调递减;
时,f(x)在(﹣∞,+∞)上单调递减;
当a∈(﹣∞,﹣ ![]() )时,f(x)在(﹣∞,﹣
)时,f(x)在(﹣∞,﹣ ![]() )上是减函数,在(﹣
)上是减函数,在(﹣ ![]() ,0)上是增函数,在(0,+∞)上是减函数
,0)上是增函数,在(0,+∞)上是减函数
(2)解:令h(x)=f(x)﹣g(x)=(﹣x2+x﹣1)ex﹣( ![]() x3+
x3+ ![]() x2+m),
x2+m),
则h′(x)=(﹣2x+1)ex+(﹣x2+x﹣1)ex﹣(x2+x)=﹣(ex+1)(x2+x)
令h′(x)>0得﹣1<x<0,令h′(x)<0得x>0或x<﹣1.
∴h(x)在x=﹣1处取得极小值h(﹣1)=﹣ ![]() ﹣
﹣ ![]() ﹣m,在x=0处取得极大值h(0)=﹣1﹣m,
﹣m,在x=0处取得极大值h(0)=﹣1﹣m,
∵函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,
∴ ![]() 即
即 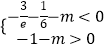 ,
,
解得:﹣ ![]() ﹣
﹣ ![]() <m<﹣1
<m<﹣1
【解析】(1)先求出函数f(x)的导函数f'(x),然后讨论a与0的大小关系,在函数的定义域内解不等式f'(x)>0和f'(x)<0,即可求出函数f(x)的单调区间;(2)令h(x)=f(x)﹣g(x),求出导数,求出单调区间,和极值,函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,即有h(﹣1)<0,且h(0)>0,解出即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的零点与方程根的关系的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能正确解答此题.
在这个区间单调递减;二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆经过点A(0,2)和B(1,1),且圆心C在直线l:x+y+5=0上.
(1)求圆C的标准方程;
(2)若P(x,y)是圆C上的动点,求3x﹣4y的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=2sin(2x+ ![]() )的图象,只需把函数y=2sinx的图象( )
)的图象,只需把函数y=2sinx的图象( )
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标变为原来的2倍(纵坐标不变)
个单位长度,再把所得各点的横坐标变为原来的2倍(纵坐标不变)
B.向左平移 ![]() 个单位长度,再把所得各点的横坐标变为原来的
个单位长度,再把所得各点的横坐标变为原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
C.各点的纵坐标不变、横坐标变为原来的2倍,再把所得图象向左平移 ![]() 个单位长度
个单位长度
D.各点的纵坐标不变、横坐标变为原来的 ![]() 倍,再把所得图象向左平移
倍,再把所得图象向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosA﹣ ![]() sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是等差数列,数列{an}的前n项和为Sn , {bn}是各项都为正数的等比数列,且a1=b1=1,a3+b2=7,S2+b2=6 (Ⅰ)求{an},{bn}的通项公式;
(Ⅱ)求数列{anbn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的右焦点在直线
)的右焦点在直线![]() :
: ![]() 上,且椭圆上任意两个关于原点对称的点与椭圆上任意一点的连线的斜率之积为
上,且椭圆上任意两个关于原点对称的点与椭圆上任意一点的连线的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]() 有两个交点
有两个交点![]() ,
, ![]() ,是否存在直线
,是否存在直线![]() :
: ![]() (其中
(其中![]() )使得
)使得![]() ,
, ![]() 到
到![]() 的距离
的距离![]() ,
, ![]() 满足
满足![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点A(2,5),B(-2,1),M(在第一象限)和N是过原点的直线l上的两个动点,且|MN|=![]() ,l∥AB,如果直线AM和BN的交点C在y轴上,求点C的坐标.
,l∥AB,如果直线AM和BN的交点C在y轴上,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com