
ЁОЬтФПЁПФГЕиЧјЙЄЛсРћгУЁАНЁВНаа![]() ЁБПЊеЙУїФъНЁВНзпЛ§ЗжНБРјЛюЖЏ.ЛсдБУПЬьзп5ЧЇВНПЩЛёЛ§Зж30Зж(ВЛзу5ЧЇВНВЛЛ§Зж)ЃЌУПЖрзп2ЧЇВНдйЛ§20Зж(ВЛзу2ЧЇВНВЛЛ§Зж).ЮЊСЫНтЛсдБЕФНЁВНзпЧщПіЃЌЙЄЛсдкФГЬьДгЯЕЭГжаЫцЛњГщШЁСЫ1000УћЛсдБЃЌЭГМЦСЫЕБЬьЫћУЧЕФВНЪ§ЃЌВЂНЋбљБОЪ§ОнЗжЮЊ
ЁБПЊеЙУїФъНЁВНзпЛ§ЗжНБРјЛюЖЏ.ЛсдБУПЬьзп5ЧЇВНПЩЛёЛ§Зж30Зж(ВЛзу5ЧЇВНВЛЛ§Зж)ЃЌУПЖрзп2ЧЇВНдйЛ§20Зж(ВЛзу2ЧЇВНВЛЛ§Зж).ЮЊСЫНтЛсдБЕФНЁВНзпЧщПіЃЌЙЄЛсдкФГЬьДгЯЕЭГжаЫцЛњГщШЁСЫ1000УћЛсдБЃЌЭГМЦСЫЕБЬьЫћУЧЕФВНЪ§ЃЌВЂНЋбљБОЪ§ОнЗжЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ОХзщЃЌећРэЕУЕНШчЯТЦЕТЪЗжВМжБЗНЭМЃК
ОХзщЃЌећРэЕУЕНШчЯТЦЕТЪЗжВМжБЗНЭМЃК
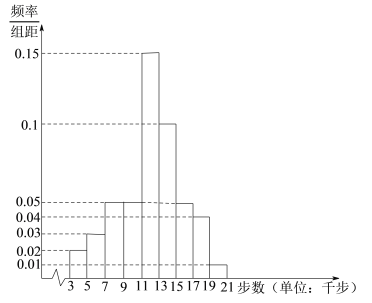
ЃЈ1ЃЉДгЕБЬьВНЪ§дк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФЛсдБжаАДЗжВуГщбљЕФЗНЪНГщШЁ6ШЫЃЌдйДгет6ШЫжаЫцЛњГщШЁ2ШЫЃЌЧѓет2ШЫЛ§ЗжжЎКЭВЛЩйгк220ЗжЕФИХТЪЃЛ
ЕФЛсдБжаАДЗжВуГщбљЕФЗНЪНГщШЁ6ШЫЃЌдйДгет6ШЫжаЫцЛњГщШЁ2ШЫЃЌЧѓет2ШЫЛ§ЗжжЎКЭВЛЩйгк220ЗжЕФИХТЪЃЛ
ЃЈ2ЃЉЧѓИУзщЪ§ОнЕФжаЮЛЪ§.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЗжВуГщбљЕФБШР§ЪНПЩжЊЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФЛсдБжаЃЌЗжБ№ГщШЁ3ШЫЃЌ2ШЫЃЌ1ШЫЃЌМЦЫуЯргІЛ§ЗжЮЊ90ЗжЃЌ110ЗжЃЌ130ЗжЃЌдђПЩвРОнЬтвтЧѓГіИХТЪЃЛ
ЕФЛсдБжаЃЌЗжБ№ГщШЁ3ШЫЃЌ2ШЫЃЌ1ШЫЃЌМЦЫуЯргІЛ§ЗжЮЊ90ЗжЃЌ110ЗжЃЌ130ЗжЃЌдђПЩвРОнЬтвтЧѓГіИХТЪЃЛ
ЃЈ2ЃЉевГіИХТЪЮЊ0.5ЪБЃЌЖдгІЕФВНЪ§МДПЩЃЌВНЪ§ЮЊ![]() ЪБЖдгІЕФИХТЪЮЊЃК
ЪБЖдгІЕФИХТЪЮЊЃК![]() ЃЌЙЪИХТЪЮЊ0.5ЪБЖдгІВНЪ§ЃЌПЩАДБШР§ЧѓЃЌЮЊ
ЃЌЙЪИХТЪЮЊ0.5ЪБЖдгІВНЪ§ЃЌПЩАДБШР§ЧѓЃЌЮЊ![]()
ЃЈ1ЃЉАДЗжВуГщбљЕФЗНЗЈЃЌдк![]() гІГщШЁ3ШЫЃЌ
гІГщШЁ3ШЫЃЌ
МЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌУПШЫЕФЛ§ЗжЪЧ90ЗжЃЛ
ЃЌУПШЫЕФЛ§ЗжЪЧ90ЗжЃЛ
дк![]() ФкгІГщШЁ2ШЫЃЌМЧЮЊ
ФкгІГщШЁ2ШЫЃЌМЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌУПШЫЕФЛ§ЗжЪЧ110ЗжЃЛ
ЃЌУПШЫЕФЛ§ЗжЪЧ110ЗжЃЛ
дк![]() гІГщШЁ1ШЫЃЌМЧЮЊcЃЌУПШЫЕФЛ§ЗжЪЧ130 ЗжЃЛ
гІГщШЁ1ШЫЃЌМЧЮЊcЃЌУПШЫЕФЛ§ЗжЪЧ130 ЗжЃЛ
Дг6ШЫжаЫцЛњГщШЁ2ШЫЃЌга![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЙВ15жжЗНЗЈ.
ЙВ15жжЗНЗЈ.
ЫљвдДг6ШЫжаЫцЛњГщШЁ2ШЫЃЌет2ШЫЕФЛ§ЗжжЎКЭВЛЩйгк220ЗжЕФга![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЙВ 6 жжЗНЗЈ.
ЙВ 6 жжЗНЗЈ.
ЩшДг6ШЫжаЫцЛњГщШЁ2ШЫЃЌет2ШЫЕФЛ§ЗжжЎКЭВЛЩйгк220ЗжЮЊЪТМўAЃЌ
дђ![]() .
.
ЃЈ2ЃЉЁпЕБВНЪ§ЮЊ![]() ЪБЖдгІЕФШЫЪ§ЫљеМБШР§ЮЊЃК
ЪБЖдгІЕФШЫЪ§ЫљеМБШР§ЮЊЃК![]()
ЁржЛашевГі![]() жаШЫЪ§еМ0.2ЪБЫљЖдгІЕФВНЪ§МДПЩ
жаШЫЪ§еМ0.2ЪБЫљЖдгІЕФВНЪ§МДПЩ
ЁрЦфВНЪ§ЮЊЃК11+![]() ЮЊЦфжаЮЛЪ§.
ЮЊЦфжаЮЛЪ§.


 ЭѕКѓалбЇАИНЬВФЭъШЋНтЖСЯЕСаД№АИ
ЭѕКѓалбЇАИНЬВФЭъШЋНтЖСЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() ЕФзюаЁе§жмЦкЮЊ
ЕФзюаЁе§жмЦкЮЊ![]() ЃЌЧвЦфЭМЯѓЙигкжБЯп
ЃЌЧвЦфЭМЯѓЙигкжБЯп![]() ЖдГЦЃЌдђдкЯТУцНсТлжае§ШЗЕФИіЪ§ЪЧ__________.
ЖдГЦЃЌдђдкЯТУцНсТлжае§ШЗЕФИіЪ§ЪЧ__________.
ЂйЭМЯѓЙигкЕу![]() ЖдГЦЃЛЂкЭМЯѓЙигкЕу
ЖдГЦЃЛЂкЭМЯѓЙигкЕу![]() ЖдГЦЃЛЂлдк
ЖдГЦЃЛЂлдк![]() ЩЯЪЧдіКЏЪ§ЃЛЂмдк
ЩЯЪЧдіКЏЪ§ЃЛЂмдк![]() ЩЯЪЧдіКЏЪ§ЃЛЂнгЩ
ЩЯЪЧдіКЏЪ§ЃЛЂнгЩ![]() ПЩЕУ
ПЩЕУ![]() БиЪЧ
БиЪЧ![]() ЕФећЪ§БЖ.
ЕФећЪ§БЖ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВЃК![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]() ЃЌдВ
ЃЌдВ![]() ЕФдВаФгыЭждВCЕФЩЯЖЅЕужиКЯЃЌЕуPЕФзнзјБъЮЊ
ЕФдВаФгыЭждВCЕФЩЯЖЅЕужиКЯЃЌЕуPЕФзнзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЭждВCЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉШєаБТЪЮЊ2ЕФжБЯпlгыЭждВCНЛгкAЃЌBСНЕуЃЌЬНОПЃКдкЭждВCЩЯЪЧЗёДцдквЛЕуQЃЌЪЙЕУ![]() ЃЌШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЌШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєІСЪЧЕквЛЯѓЯоНЧЃЌдђsinІС+cosІСЕФжЕгы1ЕФДѓаЁЙиЯЕЪЧЃЈ ЃЉ
A. sinІС+cosІСЃО1B. sinІС+cosІС=1C. sinІС+cosІСЃМ1D. ВЛФмШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬЃЉ
вбжЊЧњЯпCЕФМЋзјБъЗНГЬЪЧІб=2cosІШЃЌвдМЋЕуЮЊЦНУцжБНЧзјБъЯЕЕФдЕуЃЌМЋжсЮЊxжсЕФе§АыжсЃЌНЈСЂЦНУцжБНЧзјБъЯЕЃЌжБЯпLЕФВЮЪ§ЗНГЬЪЧ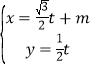 ЃЈtЮЊВЮЪ§ЃЉЃЎ
ЃЈtЮЊВЮЪ§ЃЉЃЎ
ЃЈ1ЃЉЧѓЧњЯпCЕФжБНЧзјБъЗНГЬКЭжБЯпLЕФЦеЭЈЗНГЬЃЛ
ЃЈ2ЃЉЩшЕуPЃЈmЃЌ0ЃЉЃЌШєжБЯпLгыЧњЯпCНЛгкAЃЌBСНЕуЃЌЧв|PA||PB|=1ЃЌЧѓЪЕЪ§mЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ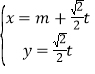 ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЭждВ
жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЭждВ![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌЦфзѓНЙЕу
ЃЌЦфзѓНЙЕу![]() дкжБЯп
дкжБЯп![]() ЩЯ.
ЩЯ.
ЃЈ1ЃЉШєжБЯп![]() гыЭждВ
гыЭждВ![]() НЛгк
НЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓЭждВ![]() ЕФФкНгОиаЮУцЛ§ЕФзюДѓжЕ.
ЕФФкНгОиаЮУцЛ§ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
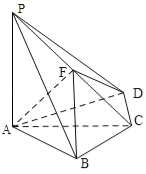
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖPЉABCDжаЃЌPAЁЭЕзУцABCDЃЌBC=CD=2ЃЌAC=4ЃЌЁЯACB=ЁЯACD=![]() ЃЌFЮЊPCЕФжаЕуЃЌAFЁЭPBЃЎ
ЃЌFЮЊPCЕФжаЕуЃЌAFЁЭPBЃЎ
ЃЈ1ЃЉЧѓPAЕФГЄЃЛ
ЃЈ2ЃЉЧѓЖўУцНЧBЉAFЉDЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() ЕФЗНИёБэжаЃЌУПИіИёБЛШОЩЯКьЁЂРЖЁЂЛЦЁЂТЬЫФжжбеЩЋжЎвЛЃЌШєУПИі
ЕФЗНИёБэжаЃЌУПИіИёБЛШОЩЯКьЁЂРЖЁЂЛЦЁЂТЬЫФжжбеЩЋжЎвЛЃЌШєУПИі![]() ЕФзгЗНИёБэАќКЌУПжжбеЩЋЕФИёОљЮЊвЛЃЌГЦДЫШОЗЈЮЊЁАОљКтЁБЕФЃЎдђЫљгаВЛЭЌЕФОљКтЕФШОЗЈга__________жжЃЎ
ЕФзгЗНИёБэАќКЌУПжжбеЩЋЕФИёОљЮЊвЛЃЌГЦДЫШОЗЈЮЊЁАОљКтЁБЕФЃЎдђЫљгаВЛЭЌЕФОљКтЕФШОЗЈга__________жжЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() ЁЃ
ЁЃ
Ђё.ЧѓКЏЪ§![]() ЕФзюаЁе§жмЦкКЭЕЅЕїЕндіЧјМфЃЛ
ЕФзюаЁе§жмЦкКЭЕЅЕїЕндіЧјМфЃЛ
Ђђ.ЕБ![]() ЪБЃЌЗНГЬ
ЪБЃЌЗНГЬ![]() ЧЁгаСНИіВЛЭЌЕФЪЕЪ§ИљЃЌЧѓЪЕЪ§
ЧЁгаСНИіВЛЭЌЕФЪЕЪ§ИљЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
Ђѓ.НЋКЏЪ§![]() ЕФЭМЯѓЯђгвЦНвЦ
ЕФЭМЯѓЯђгвЦНвЦ![]() ИіЕЅЮЛКѓЫљЕУКЏЪ§
ИіЕЅЮЛКѓЫљЕУКЏЪ§![]() ЕФЭМЯѓЙигкдЕужааФЖдГЦЃЌЧѓ
ЕФЭМЯѓЙигкдЕужааФЖдГЦЃЌЧѓ![]() ЕФзюаЁжЕЁЃ
ЕФзюаЁжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com