
【题目】已知函数f(x)= ![]() ,g(x)=ax﹣3.
,g(x)=ax﹣3.
(1)当a=l时,确定函数h(x)=f(x)﹣g(x)在(0,+∞)上的单调性;
(2)若对任意x∈[0,4],总存在x0∈[﹣2,2],使得g(x0)=f(x)成立,求 实数a的取值范围.
【答案】
(1)解:由题意:当a=l时,确定函数h(x)=f(x)﹣g(x)=)= ![]() ﹣x+3.
﹣x+3.
∵x∈(0,+∞)
则 ![]() =
= ![]() >0,
>0,
∴h(x)在(0,+∞)上是单调增函数
(2)解:由题意:x∈[0,4]上函数f(x)= ![]() 的值域M=[3,5],
的值域M=[3,5],
设函数g(x)=ax﹣3的值域N.
∵x0∈[﹣2,2],g(x)=ax﹣3.
当a=0时,g(x)=﹣3,即值域N={﹣3},
∵MN,
∴不满足题意.
当a>0时,函数g(x)在定义域内为增函数,其值域N=[﹣2a﹣3,2a﹣3],
∵MN,
∴需满足 ![]() ,
,
解得:a≥4.
当a<0时,函数g(x)在定义域内为减函数,其值域N=[2a﹣3,﹣2a﹣3],
∵MN,
∴需满足 ![]()
解得:a≤﹣4.
综上所得:对任意x∈[0,4],总存在x0∈[﹣2,2],使得g(x0)=f(x)成立,
实数a的取值范围是(﹣∞,﹣4]∪[4,+∞)
【解析】(1)由题意:当a=l时,确定函数h(x)=f(x)﹣g(x)=)= ![]() ﹣x+3.判断x在(0,+∞)上
﹣x+3.判断x在(0,+∞)上 ![]() 与x的大小可得单调性.(2)求解x∈[0,4]上函数f(x)=
与x的大小可得单调性.(2)求解x∈[0,4]上函数f(x)= ![]() 的值域M,x0∈[﹣2,2]上,对a讨论函数g(x)=ax﹣3的值域N,
的值域M,x0∈[﹣2,2]上,对a讨论函数g(x)=ax﹣3的值域N,
根据MN,可得实数a的取值范围.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x>0时,函数f(x)的解析式为![]() .
.
(1)求当x<0时函数f(x)的解析式;
(2)用定义证明f(x)在(0,+∞)上的是减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AB=2,AD=1,E,F,G分别是DD1 , AB,CC1的中点,则异面直线A1E与GF所成角为( ) 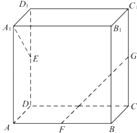
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
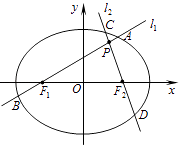
【题目】分别过椭圆E: ![]() =1(a>b>0)左、右焦点F1、F2的动直线l1、l2相交于P点,与椭圆E分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率分别为k1、k2、k3、k4 , 且满足k1+k2=k3+k4 , 已知当l1与x轴重合时,|AB|=2
=1(a>b>0)左、右焦点F1、F2的动直线l1、l2相交于P点,与椭圆E分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率分别为k1、k2、k3、k4 , 且满足k1+k2=k3+k4 , 已知当l1与x轴重合时,|AB|=2 ![]() ,|CD|=
,|CD|= ![]() .
. 
(1)求椭圆E的方程;
(2)是否存在定点M,N,使得|PM|+|PN|为定值?若存在,求出M、N点坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S. ①当 ![]() 时,S为四边形
时,S为四边形
②截面在底面上投影面积恒为定值 ![]()
③不存在某个位置,使得截面S与平面A1BD垂直
④当 ![]() 时,S与C1D1的交点满足C1R1=
时,S与C1D1的交点满足C1R1= ![]()
其中正确命题的个数为 ( )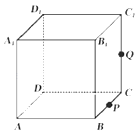
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的两个焦点为![]() ,
, ![]() 是椭圆上一点,若
是椭圆上一点,若![]() ,
, ![]() .
.
(1)求椭圆的方程;
(2)直线![]() 过右焦点
过右焦点![]() (不与
(不与![]() 轴重合)且与椭圆相交于不同的两点
轴重合)且与椭圆相交于不同的两点![]() ,在
,在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() ,使得
,使得![]() 的值为定值?若存在,写出
的值为定值?若存在,写出![]() 点的坐标(不必求出定值);若不存在,说明理由.
点的坐标(不必求出定值);若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com