
【题目】设p:实数x满足x2-2(a+1)x+2a+a2<0,q:实数x满足![]()
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)把![]() 代入不等式后求解不等式,同时求解不等式组,得到命题
代入不等式后求解不等式,同时求解不等式组,得到命题![]() 和命题
和命题![]() 中
中![]() 的取值范围,由
的取值范围,由![]() 且
且![]() 为真,对求得的两个范围求交集即可;(2)
为真,对求得的两个范围求交集即可;(2)![]() 是
是![]() 的必要不充分条件,则集合
的必要不充分条件,则集合![]() 是集合
是集合![]() 的子集,分类讨论后运用区间端点值之间的关系可求的
的子集,分类讨论后运用区间端点值之间的关系可求的![]() 取值范围.
取值范围.
(1)由x2-2(a+1)x+a+a2<0得(x-(a+2))(x-a)<0,
当a=1时,解得1<x<3,即p为真时实数x的取值范围是1<x<3.
由![]() 得2<x≤3,即q为真时实数x的取值范围是2<x≤3.
得2<x≤3,即q为真时实数x的取值范围是2<x≤3.
若p∧q为真,则p真且q真,所以实数x的取值范围是(2,3).
(2)p是q的必要不充分条件, A=(a,a+2),B=(2,3],故有![]()
解得1<a≤2;所以实数a的取值范围是(1,2].


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若直线ax+by—4=0和圆x2+y2=4没有公共点,则过点(a,b)的直线与椭圆![]() +
+![]() =1的公共点个数为( )
=1的公共点个数为( )
A. 0 B. 1 C. 2 D. 由a,b的取值来确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,若
中,若![]() 是线段
是线段![]() 上的动点,则下列结论不正确的是( )
上的动点,则下列结论不正确的是( )
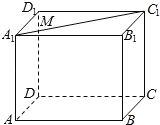
A. 三棱锥![]() 的正视图面积是定值
的正视图面积是定值
B. 异面直线![]() ,
,![]() 所成的角可为
所成的角可为![]()
C. 异面直线![]() ,
,![]() 所成的角为
所成的角为![]()
D. 直线![]() 与平面
与平面![]() 所成的角可为
所成的角可为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方造一千多年,例如堑堵指底面为直角三角形,且测量垂直底面的三棱柱,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,如图,在堑堵![]() 中,
中,![]() ,若当阳马
,若当阳马![]() 的体积最大时,则堑堵
的体积最大时,则堑堵![]() 的体积为__________
的体积为__________

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF ![]() 2CE,G是线段BF上一点,AB=AF=BC=2.
2CE,G是线段BF上一点,AB=AF=BC=2. 
(1)当GB=GF时,求证:EG∥平面ABC;
(2)求二面角E﹣BF﹣A的余弦值;
(3)是否存在点G满足BF⊥平面AEG?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 是直线
是直线![]() 上一动点,过点
上一动点,过点![]() 作圆的切线
作圆的切线![]()
(1)当![]() 的横坐标为2时,求切线方程;
的横坐标为2时,求切线方程;
(2)求证:经过![]() 三点的圆
三点的圆![]() 必过定点,并求此定点的坐标;
必过定点,并求此定点的坐标;
(3)当线段![]() 长度最小时,求四边形
长度最小时,求四边形![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
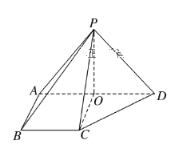
(1)求B点到平面PCD的距离;
(2)线段PD上是否存在一点Q,使得二面角Q-AC-D的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生更多的了解“数学史”知识,梁才学校高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:
序号 | 分组 | 组中值 | 频数 | 频率 |
(i) | (分数) | (Gi) | (人数) | (Fi) |
1 |
| 65 | ① | 0.12 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.24 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1 | ||
(1)填充频率分布表中的空格;
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于85分的同学能获奖,请估计在
参加的800名学生中大概有多少名学生获奖?(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的S的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com