
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过原点
,过原点![]() 且斜率为1的直线
且斜率为1的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,四边形
两点,四边形![]() 的周长与面积分别为8与
的周长与面积分别为8与![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,求证:
,求证:![]() 到直线
到直线![]() 的距离为定值.
的距离为定值.
 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】城镇化是国家现代化的重要指标,据有关资料显示,1978—2013年,我国城镇常住人口从1.7亿增加到7.3亿.假设每一年城镇常住人口的增加量都相等,记1978年后第t(限定![]() )年的城镇常住人口为
)年的城镇常住人口为![]() 亿.写出
亿.写出![]() 的解析式,并由此估算出我国2017年的城镇常住人口数.
的解析式,并由此估算出我国2017年的城镇常住人口数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为![]() (
(![]() 为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=
为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=![]() 时,这两个交点重合.
时,这两个交点重合.
(1) 求曲线C1,C2的直角坐标方程
(2) 设当 α=![]() 时,l与C1,C2的交点分别为A1,B1,当 α=-
时,l与C1,C2的交点分别为A1,B1,当 α=-![]() 时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在本市某旧小区改造工程中,需要在地下铺设天燃气管道.已知小区某处三幢房屋分别位于扇形![]() 的三个顶点上,点
的三个顶点上,点![]() 是弧
是弧![]() 的中点,现欲在线段
的中点,现欲在线段![]() 上找一处开挖工作坑
上找一处开挖工作坑![]() (不与点
(不与点![]() ,
,![]() 重合),为铺设三条地下天燃气管线
重合),为铺设三条地下天燃气管线![]() ,
,![]() ,
,![]() ,已知
,已知![]() 米,
米,![]() ,记
,记![]() ,该三条地下天燃气管线的总长度为
,该三条地下天燃气管线的总长度为![]() 米.
米.

(1)将![]() 表示成
表示成![]() 的函数,并写出
的函数,并写出![]() 的范围;
的范围;
(2)请确定工作坑![]() 的位置,使此处地下天燃气管线的总长度最小,并求出总长度的最小值.
的位置,使此处地下天燃气管线的总长度最小,并求出总长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是AC的中点,四边形BDEF是菱形,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() .
.
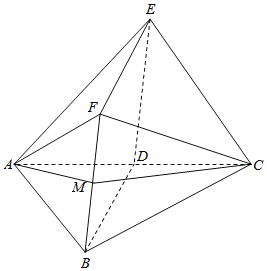
![]() 若点M是线段BF的中点,证明:
若点M是线段BF的中点,证明:![]() 平面AMC;
平面AMC;
![]() 求平面AEF与平面BCF所成的锐二面角的余弦值.
求平面AEF与平面BCF所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量y(单位:万只)与相成年份x(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数z(单位:个)关于x的回归方程![]() .
.

(1)根据表中的数据和所给统计量,求y关于x的线性回归方程(参考统计量:![]() );
);
(2)试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中国决胜全面建成小康社会的关键之年,如何更好地保障和改善民生,如何切实增强政策“获得感”,成为![]() 年全国两会的重要关切.某地区为改善民生调研了甲、乙、丙、丁、戊
年全国两会的重要关切.某地区为改善民生调研了甲、乙、丙、丁、戊![]() 个民生项目,得到如下信息:①若该地区引进甲项目,就必须引进与之配套的乙项目;②丁、戊两个项目与民生密切相关,这两个项目至少要引进一个;③乙、丙两个项目之间有冲突,两个项目只能引进一个;④丙、丁两个项目关联度较高,要么同时引进,要么都不引进;⑤若引进项目戊,甲、丁两个项目也必须引进.则该地区应引进的项目为( )
个民生项目,得到如下信息:①若该地区引进甲项目,就必须引进与之配套的乙项目;②丁、戊两个项目与民生密切相关,这两个项目至少要引进一个;③乙、丙两个项目之间有冲突,两个项目只能引进一个;④丙、丁两个项目关联度较高,要么同时引进,要么都不引进;⑤若引进项目戊,甲、丁两个项目也必须引进.则该地区应引进的项目为( )
A. 甲、乙B. 丙、丁C. 乙、丁D. 甲、丙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :关于
:关于![]() 的不等式
的不等式![]() 无解;命题
无解;命题![]() :指数函数
:指数函数![]() 是
是![]() 上的增函数.
上的增函数.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若满足![]() 为假命题且
为假命题且![]() 为真命题的实数
为真命题的实数![]() 取值范围是集合
取值范围是集合![]() ,集合
,集合![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com