
【题目】如图,在四棱锥![]() 中,
中,![]() 为等边三角形,
为等边三角形,![]()
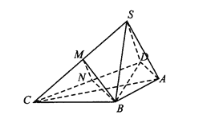
(1)若点![]() 分别是线段
分别是线段![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 为直二面角,求直线
为直二面角,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据等腰三角形三线合一和已知的角度和边长关系可证得![]() ,从而可知
,从而可知![]() ;在利用三角形中位线可证得
;在利用三角形中位线可证得![]() ;根据线面平行判定定理和面面平行判定定理可证得结论;(2)设
;根据线面平行判定定理和面面平行判定定理可证得结论;(2)设![]() 交
交![]() 于点
于点![]() ,利用面面垂直的性质定理可证得
,利用面面垂直的性质定理可证得![]() 平面
平面![]() ,从而可建立起空间直角坐标系;利用线面角的向量求法可求得结果.
,从而可建立起空间直角坐标系;利用线面角的向量求法可求得结果.
(1)![]() 为等边三角形,且
为等边三角形,且![]() 是线段
是线段![]() 的中点
的中点 ![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 点
点![]() 分别是线段
分别是线段 的中点
的中点 ![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
![]()
![]() 平面
平面![]() 平面
平面![]()
(2)设![]() 交
交![]() 于点
于点![]() ,连接
,连接![]()
由对称性知,![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]()
![]() 二面角
二面角![]() 为直二面角
为直二面角 ![]() 平面
平面![]()
不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() /p>
/p>
以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,建立如图所示空间直角坐标系
轴,建立如图所示空间直角坐标系
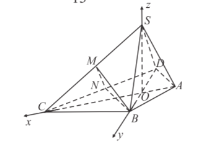
则![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]()
则 ,即:
,即: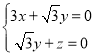
令![]() ,得
,得![]() ,
,![]()
![]()

![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是函数
是函数![]() 的导函数,且
的导函数,且![]() ,
,![]() ,则下列说法正确的是___________.
,则下列说法正确的是___________.
①![]() ;
;
②曲线![]() 在
在![]() 处的切线斜率最小;
处的切线斜率最小;
③函数![]() 在
在![]() 存在极大值和极小值;
存在极大值和极小值;
④![]() 在区间
在区间![]() 上至少有一个零点.
上至少有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机厂商在销售200万台某型号手机时开展“手机碎屏险”活动、活动规则如下:用户购买该型号手机时可选购“手机碎屏险”,保费为![]() 元,若在购机后一年内发生碎屏可免费更换一次屏幕.该手机厂商将在这
元,若在购机后一年内发生碎屏可免费更换一次屏幕.该手机厂商将在这![]() 万台该型号手机全部销售完毕一年后,在购买碎屏险且购机后一年内未发生碎屏的用户中随机抽取
万台该型号手机全部销售完毕一年后,在购买碎屏险且购机后一年内未发生碎屏的用户中随机抽取![]() 名,每名用户赠送
名,每名用户赠送![]() 元的红包,为了合理确定保费
元的红包,为了合理确定保费![]() 的值,该手机厂商进行了问卷调查,统计后得到下表(其中
的值,该手机厂商进行了问卷调查,统计后得到下表(其中![]() 表示保费为
表示保费为![]() 元时愿意购买该“手机碎屏险”的用户比例);
元时愿意购买该“手机碎屏险”的用户比例);
(1)根据上面的数据求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)通过大数据分析,在使用该型号手机的用户中,购机后一年内发生碎屏的比例为![]() .已知更换一次该型号手机屏幕的费用为
.已知更换一次该型号手机屏幕的费用为![]() 元,若该手机厂商要求在这次活动中因销售该“手机碎屏险”产生的利润不少于
元,若该手机厂商要求在这次活动中因销售该“手机碎屏险”产生的利润不少于![]() 万元,能否把保费
万元,能否把保费![]() 定为5元?
定为5元?
x | 10 | 20 | 30 | 40 | 50 |
y | 0.79 | 0.59 | 0.38 | 0.23 | 0.01 |
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为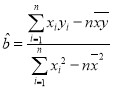 ,
,
![]() ,
,
参考数据:表中![]() 的5个值从左到右分别记为
的5个值从左到右分别记为![]() ,相应的
,相应的![]() 值分别记为
值分别记为![]() ,经计算有
,经计算有![]() ,其中
,其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2020年举行促销活动,经调查测算,某产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元,满足
万元,满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2020年该产品的利润![]() (万元)表示为年促销费用
(万元)表示为年促销费用![]() (万元)的函数;
(万元)的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,设直线
,设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 为线段
为线段![]() 的中点.
的中点.

(1)若直线![]() 的倾斜角为
的倾斜角为![]() ,求
,求![]() 的值;
的值;
(2)设直线![]() 交直线
交直线![]() 于点
于点![]() ,证明:直线
,证明:直线![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个暗箱中有形状和大小完全相同的3只白球与2只黑球,每次从中取出一只球,取到白球得2分,取到黑球得3分.甲从暗箱中有放回地依次取出3只球.
(1)求甲三次都取得白球的概率;
(2)求甲总得分ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com