
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,设直线
,设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 为线段
为线段![]() 的中点.
的中点.

(1)若直线![]() 的倾斜角为
的倾斜角为![]() ,求
,求![]() 的值;
的值;
(2)设直线![]() 交直线
交直线![]() 于点
于点![]() ,证明:直线
,证明:直线![]() .
.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)设![]() ,根据图形可知
,根据图形可知![]() ,直线
,直线![]() 的方程为
的方程为![]() ,代入椭圆方程得到根与系数的关系,
,代入椭圆方程得到根与系数的关系,![]() ,这样可求得三角形的面积;(2)设直线
,这样可求得三角形的面积;(2)设直线![]() 的方程为
的方程为![]() 与椭圆方程联立,得到根与系数的关系,再根据
与椭圆方程联立,得到根与系数的关系,再根据![]() 三点共线,那么
三点共线,那么![]() ,得到坐标间的关系,若
,得到坐标间的关系,若![]() ,即说明
,即说明![]() .
.
试题解析:由题意,知![]() ,.........1分
,.........1分
(1)∵直线![]() 的倾斜角为
的倾斜角为![]() ,∴
,∴![]() .........................1分
.........................1分
∴直线![]() 的方程为
的方程为![]() ......................2分
......................2分
代入椭圆方程,可得![]() .
.
设![]() .∴
.∴![]() ........................4分
........................4分
∴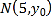 ............6分
............6分
(2)设直线![]() 的方程为
的方程为![]() .
.
代入椭圆方程,得![]() .
.
设![]() ,则
,则![]() ...............8分
...............8分
设![]() ,∵
,∵![]() 三点共线,
三点共线,
∴有![]() ,∴
,∴![]() ...........................9分
...........................9分
而![]()
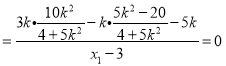 ...................11分
...................11分
∴直线![]() 轴,即
轴,即![]() ..............................12分
..............................12分


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,设椭圆
中,设椭圆![]() 的左焦点为
的左焦点为![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() ,且
,且![]() ,点
,点![]() 在
在![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 和圆
和圆![]() 分别相切于
分别相切于![]() ,
,![]() 两点,当
两点,当![]() 面积取得最大值时,求直线
面积取得最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点 ,若点
,若点![]() 在椭圆C上,则点
在椭圆C上,则点![]() 称为点M的一个“椭点”.
称为点M的一个“椭点”.
(1)求椭圆C的标准方程;
(2)若直线![]() 与椭圆C相交于A,B两点,且A,B两点的“椭点”分别为P,Q,以PQ为直径的圆经过坐标原点,试判断
与椭圆C相交于A,B两点,且A,B两点的“椭点”分别为P,Q,以PQ为直径的圆经过坐标原点,试判断![]() 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由;
的值,并说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点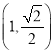 ,
,![]() 是该椭圆的左、右焦点,
是该椭圆的左、右焦点,![]() 是上顶点,且
是上顶点,且![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求![]() 的方程;
的方程;
(2)已知![]() 是坐标原点,直线
是坐标原点,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,点
两点,点![]() 在
在![]() 上且满足四边形
上且满足四边形![]() 是一个平行四边形,求
是一个平行四边形,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分为五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意).其统计结果如下表(住宿满意度为![]() ,餐饮满意度为
,餐饮满意度为![]() )
)
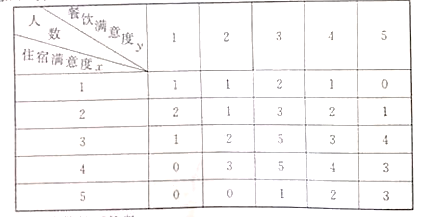
(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
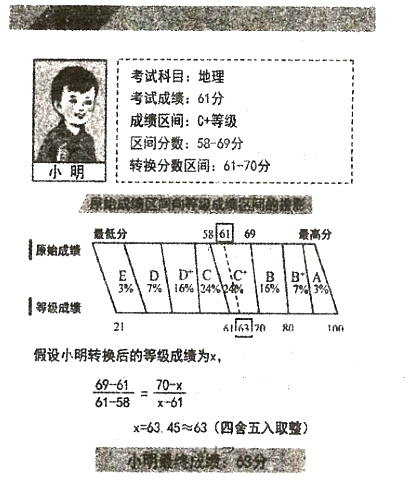
【题目】《山东省高考改革试点方案》规定:从![]() 年高考开始,高考物理、化学等六门选考科目的考生原始成绩从高到低划分为
年高考开始,高考物理、化学等六门选考科目的考生原始成绩从高到低划分为![]() 八个等级.参照正态分布原则,确定各等级人数所占比例分别为
八个等级.参照正态分布原则,确定各等级人数所占比例分别为![]() .选考科目成绩计入考生总成绩时,将
.选考科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则分别转换到
等级内的考生原始成绩,依照等比例转换法则分别转换到![]()
![]() 八个分数区间,得到考生的等级成绩.
八个分数区间,得到考生的等级成绩.
某校![]() 级学生共
级学生共![]() 人,以期末考试成绩为原始成绩转换了本校的等级成绩,为学生合理选科提供依据,其中物理成绩获得等级
人,以期末考试成绩为原始成绩转换了本校的等级成绩,为学生合理选科提供依据,其中物理成绩获得等级![]() 的学生原始成绩统计如下
的学生原始成绩统计如下
成绩 | 93 | 91 | 90 | 88 | 87 | 86 | 85 | 84 | 83 | 82 |
人数 | 1 | 1 | 4 | 2 | 4 | 3 | 3 | 3 | 2 | 7 |
(1)从物理成绩获得等级![]() 的学生中任取
的学生中任取![]() 名,求恰好有
名,求恰好有![]() 名同学的等级分数不小于
名同学的等级分数不小于![]() 的概率;
的概率;
(2)待到本级学生高考结束后,从全省考生中不放回的随机抽取学生,直到抽到![]() 名同学的物理高考成绩等级为
名同学的物理高考成绩等级为![]() 或
或![]() 结束(最多抽取
结束(最多抽取![]() 人),设抽取的学生个数为
人),设抽取的学生个数为![]() ,求随机变量
,求随机变量![]() 的数学期望(注:
的数学期望(注: ![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com