Question

【题目】设函数，，其中.若函数在区间上有且仅有一个零点，则实数的取值范围是__．

Answer 1

【答案】或

【解析】

由g（x）＝f（x）﹣4mx﹣m＝0得f（x）＝4mx+m，分别作出两个函数的图象，利用数形结合建立不等式关系进行求解即可．

由题可得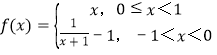．作函数y＝f（x）的图象，如图所示

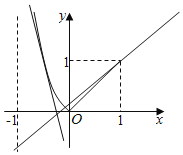
函数g（x）零点的个数函数y＝f（x）的图象与直线y＝4mx+m交点的个数．

当直线y＝4mx+m过点（1，1）时，；当直线y＝4mx+m与曲线（﹣1＜x＜0）相切时，（m＜0），

由4mx+m

得4mx+m，

即﹣x＝（4mx+m）（x+1），

整理得4mx2+（5m+1）x+m＝0，

则判别式△＝（5m+1）2﹣16m2＝0，且﹣10

即9m2+10m+1＝0，

可求得m＝﹣1或m．

当m时，﹣10不成立，

故此时m＝﹣1，

根据图象可知当m或m＝﹣1时，函数g（x）在区间（﹣1，1）上有且仅有一个零点．

故答案为或．