【题目】直线
是过点
的动直线，当与圆
相切时，同时也和抛物线
相切.
（1）求抛物线
的方程；
（2）直线与抛物线交于不同的两点
，与圆
交于不同的两点A、B，
面积为
，
面积为
，当
时，求直线的方程．
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝2|x＋1|＋|x－2|.
(1)求f(x)的最小值m；
(2)若a，b，c均为正实数，且满足a＋b＋c＝m，求证：
＋
＋
≥3.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某小区内有一块以
为圆心半径为20米的圆形区域.广场，为丰富市民的业余文化生活，现提出如下设计方案：如图，在圆形区域内搭建露天舞台，舞台为扇形
区域，其中两个端点
，
分别在圆周上；观众席为梯形
内且在圆外的区域，其中
，
，且
，
在点的同侧.为保证视听效果，要求观众席内每一个观众到舞台处的距离都不超过60米.设
.
（1）求的长（用
表示）；
（2）对于任意，上述设计方案是否均能符合要求？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定义在R上的函数
在[1，2]上有且仅有3个零点，其图象关于点
和直线x
对称，给出下列结论：
①
；
②函数f（x）在[0，1]上有且仅有3个极值点；
③函数f（x）在
上单调递增；
④函数f（x）的最小正周期是2．
其中所有正确结论的编号是（ ）
A.②③B.①④C.②③④D.①②
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝2cos2x+ax2．
（1）当a＝1时，求f（x）的导函数
在
上的零点个数；
（2）若关于x的不等式2cos（2sinx）+a2x2≤af（x）在（﹣∞，+∞）上恒成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】人口平均预期寿命是综合反映人们健康水平的基本指标.
年第六次全国人口普查资料表明，随着我国社会经济的快速发展，人民生活水平的不断提高以及医疗卫生保障体系的逐步完善，我国人口平均预期寿命继续延长，国民整体健康水平有较大幅度的提高.下图体现了我国平均预期寿命变化情况，依据此图，下列结论错误的是（ ）
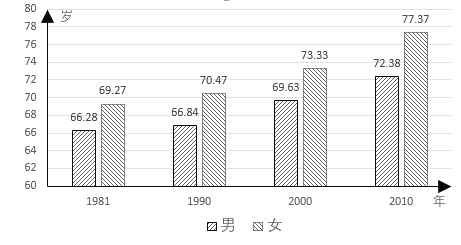
A.男性的平均预期寿命逐渐延长
B.女性的平均预期寿命逐渐延长
C.男性的平均预期寿命延长幅度略高于女性
D.女性的平均预期寿命延长幅度略高于男性
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】直线
是过点
的动直线，当与圆
相切时，同时也和抛物线
相切.
（1）求抛物线
的方程；
（2）直线与抛物线交于不同的两点
，与圆
交于不同的两点A、B，
面积为
，
面积为
，当
时，求直线的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】“未来肯定是非接触的，无感支付的方式将成为主流，这有助于降低交互门槛”.云从科技联合创始人姚志强告诉南方日报记者.相对于主流支付方式二维码支付，刷脸支付更加便利，以前出门一部手机解决所有，而现在连手机都不需要了，毕竟，手机支付还需要携带手机，打开二维码也需要时间和手机信号.刷脸支付将会替代手机，成为新的支付方式.某地从大型超市门口随机抽取50名顾客进行了调查，得到了如表列联表：
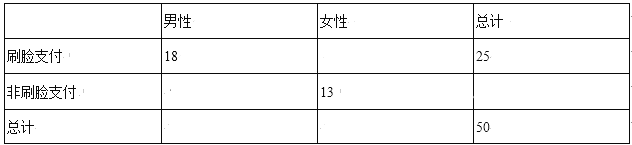
（1）请将上面的列联表补充完整，并判断是否有
的把握认为使用刷脸支付与性别有关？
（2）从参加调查且使用刷脸支付的顾客中随机抽取2人参加抽奖活动，抽奖活动规则如下：“一等奖”中奖概率为0.25，奖品为10元购物券
张（
，且
），“二等奖”中奖概率0.25，奖品为10元购物券两张，“三等奖”中奖概率0.5，奖品为10元购物券一张，每位顾客是否中奖相互独立，记参与抽奖的两位顾客中奖购物券金额总和为
元，若要使的均值不低于50元，求的最小值.
附：
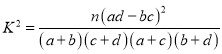，其中
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，曲线
的参数方程为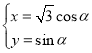
（
为参数），以原点
为极点，以
轴正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
.
（1）求曲线的普通方程与曲线的直角坐标方程；
（2）设
为曲线上位于第一，二象限的两个动点，且
，射线
交曲线分别于
，求
面积的最小值，并求此时四边形
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
