
����Ŀ���ֻ�![]() �еġ�
�еġ�![]() �˶������������Ĺ��ܣ��������Կ��Լ�ÿ����˶������������Կ�������Ȧ����ѵIJ���.С����
�˶������������Ĺ��ܣ��������Կ��Լ�ÿ����˶������������Կ�������Ȧ����ѵIJ���.С����![]() ����Ȧ���д������Ѳ����ˡ�
����Ȧ���д������Ѳ����ˡ�![]() �˶����������ѡȡ������30����������Ů��15������¼������ijһ�����·������ͳ���������±���ʾ��
�˶����������ѡȡ������30����������Ů��15������¼������ijһ�����·������ͳ���������±���ʾ��
|
|
|
|
|
|
�� | 0 | 2 | 4 | 7 | 2 |
Ů | 1 | 3 | 7 | 3 | 1 |
�����������������壬������Ƶ��Ϊ���ʣ���С��![]() ����Ȧ������Ժ���������ѡȡ3����������·��������7500������
����Ȧ������Ժ���������ѡȡ3����������·��������7500������![]() ������
������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�������ij��һ�����·��������7500�������˽�����![]() �˶�������Ϊ�������͡�������Ϊ�������͡�.����������������
�˶�������Ϊ�������͡�������Ϊ�������͡�.����������������![]() �����������ݴ��ж��ܷ���
�����������ݴ��ж��ܷ���![]() ���ϵİ�����Ϊ���������͡��롰�Ա��йأ�
���ϵİ�����Ϊ���������͡��롰�Ա��йأ�
������ | ������ | �ܼ� | |
�� | |||
Ů | |||
�ܼ� |
����![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
���𰸡�������������������
�����������������
�������������С�������Ժ���������ѡȡ1����������·��������7500�ĸ���Ϊ![]() ��
��
Ȼ���������ɵ�![]() �����п���ȡֵ�ֱ�Ϊ0��1��2��3���ֱ�������ʺ�ɵ�
�����п���ȡֵ�ֱ�Ϊ0��1��2��3���ֱ�������ʺ�ɵ�![]() �ķֲ��У�Ȼ�������������������������
�ķֲ��У�Ȼ�������������������������![]() ���������ɱ������ݵõ�
���������ɱ������ݵõ�![]() ���ʿɵ�û��
���ʿɵ�û��![]() ���ϵİ�����Ϊ���������͡��롰�Ա��йأ�
���ϵİ�����Ϊ���������͡��롰�Ա��йأ�
���������
������С�������Ժ���������ѡȡ1����������·��������7500�ĸ���Ϊ![]() .
.
�������![]() �����п���ȡֵ�ֱ�Ϊ0��1��2��3��
�����п���ȡֵ�ֱ�Ϊ0��1��2��3��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
���������![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��![]()
![]() .
.
�������![]() ������
������
������ | ������ | �ܼ� | |
�� | 9 | 6 | 15 |
Ů | 4 | 11 | 15 |
�ܼ� | 13 | 17 | 30 |
�ɱ������ݿɵ�![]()
![]() .
.
��û��![]() ���ϵİ�����Ϊ���������͡��롰�Ա��й�.
���ϵİ�����Ϊ���������͡��롰�Ա��й�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУѧ����������ѧ�о�С���ڶ�ѧ���Ͽ�ע������������ĵ����о��У���������40���ӵ�һ�ڿ��У�ע����ָ��![]() ������ʱ��
������ʱ��![]() ����λ�����ӣ�֮��Ĺ�ϵ������ͼ��ʾ�����ߣ���
����λ�����ӣ�֮��Ĺ�ϵ������ͼ��ʾ�����ߣ���![]() ʱ�������Ƕ��κ���ͼ���һ���֣���
ʱ�������Ƕ��κ���ͼ���һ���֣���![]() ʱ�������Ǻ���
ʱ�������Ǻ���![]() ͼ���һ���֣�����ר���о�����ע����ָ��
ͼ���һ���֣�����ר���о�����ע����ָ��![]() ����80ʱѧϰЧ����ѣ�
����80ʱѧϰЧ����ѣ�

��1������![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����ʦ��ʲôʱ���ڰ��ź������ݣ���ʹ��ѧ��ѧϰЧ����ѣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���f��x������f��x����ͼ���ϴ��ڹ���ԭ��ԳƵĵ㣬���f��x��Ϊ�������ϵ���α�溯������
��1����f��x����ln��2x+1��+m�Ƕ���������[��1��1]�ϵ���α�溯��������ʵ��m��ȡֵ��Χ��
��2��������f��x����4x��m2x+2+4m2��3��R���Ƿ�Ϊ��α�溯��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������̨![]() �У���
����![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��![]() �ڣ����߽磩��һ�����㣬����ƽ��
�ڣ����߽磩��һ�����㣬����ƽ��![]() ƽ��
ƽ��![]() ����
����![]() �Ĺ켣�ǣ� ��
�Ĺ켣�ǣ� ��

A. ƽ��B. ֱ��C. �߶Σ���ֻ��1���˵�D. Բ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ�У���ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ����֪����C��![]() ��a��0��������P����2����4����ֱ��l�IJ�������Ϊ
��a��0��������P����2����4����ֱ��l�IJ�������Ϊ ��tΪ��������l��C�ֱ���M��N.
��tΪ��������l��C�ֱ���M��N.
��1��д��C��ƽ��ֱ������ϵ���̺�l����ͨ���̣�
��2����|PM|��|MN|��|PN|�ɵȱ����У���a��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������E��![]() ����Ϊ
����Ϊ![]() ������Ϊ
������Ϊ![]() ��
��![]() Ϊ����ԭ�㡣
Ϊ����ԭ�㡣
��1�������![]() ��
��![]() ������
������![]() ���е�Բ�ķ��̣�
���е�Բ�ķ��̣�
��2����![]() ���ֱ�߽�������E��
���ֱ�߽�������E��![]() ���㣬��A����x��ĶԳƵ�Ϊ
���㣬��A����x��ĶԳƵ�Ϊ![]() ���ҵ�
���ҵ�![]() ���
���![]() ���غϣ���֤��ֱ��
���غϣ���֤��ֱ��![]()
![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��![]() ����Բ�ϣ���Բ����Ϊ
����Բ�ϣ���Բ����Ϊ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() �������
�������![]() �������
�������![]() ����
����
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2��ֱ��![]() ��
��![]() ������Բ
������Բ![]() ����
����![]() ��
��![]() ������
������![]() ��
��![]() ���ӳ�����Բ
���ӳ�����Բ![]() ��
��![]() ��
��![]() ������
������![]() ��ָ��
��ָ��![]() ��
��![]() ֮��Ĺ�ϵ����˵�����ɣ�
֮��Ĺ�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���ѧ�ɾ͵Ľܳ������������С�����¸������㻡��������õľ��鷽ʽΪ���������=![]() ���ҡ�ʸ+ʸ2���������ͼ����Բ��������������Χ�ɣ���ʽ�С��ҡ�ָԲ�������ҳ�����ʸ�����ڰ뾶����Բ�ĵ��ҵľ���֮�����Բ�Ľ�Ϊ
���ҡ�ʸ+ʸ2���������ͼ����Բ��������������Χ�ɣ���ʽ�С��ҡ�ָԲ�������ҳ�����ʸ�����ڰ뾶����Բ�ĵ��ҵľ���֮�����Բ�Ľ�Ϊ![]() ���뾶����
���뾶����![]() �Ļ�������������鹫ʽ�������û������Լ��
�Ļ�������������鹫ʽ�������û������Լ�� ![]()
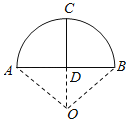
A. ![]() ƽ���� B.
ƽ���� B. ![]() ƽ����
ƽ����
C. ![]() ƽ���� D.
ƽ���� D. ![]() ƽ����
ƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����μ���ѧ������������ѧ�Ҳ�Ŭ��.![]() .���¶���������20����70���������һ����ѧ�ƣ����Ĵ�����Ϊ�����ͳ��ѧ�ڶ�����������ṩ��ȫ�µ�˼·����ͼ�ǰ���һ���ķ��ι���������һ������ͼ�����13�е�ʵ��Բ��ĸ�����______.
.���¶���������20����70���������һ����ѧ�ƣ����Ĵ�����Ϊ�����ͳ��ѧ�ڶ�����������ṩ��ȫ�µ�˼·����ͼ�ǰ���һ���ķ��ι���������һ������ͼ�����13�е�ʵ��Բ��ĸ�����______.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com