
【题目】如图:点P在直径AB=1的半圆上移动(点P不与A,B重合),过P作圆的切线PT且PT=1,∠PAB=α,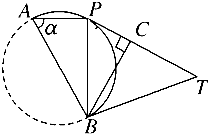
(1)当α为何值时,四边形ABTP面积最大?
(2)求|PA|+|PB|+|PC|的取值范围?
【答案】
(1)解:∵AB为直径,
∴∠APB=90°,AB=1,
∵∠PAB=α,
∴PA=cosα,PB=sinα,
又PT切圆于P点,∠TPB=∠PAB=α,
∴BC=sinαPB=sin2α,
∴S四边形ABTP=S△PAB+S△TPB
= ![]() PAPB+
PAPB+ ![]() PTBC
PTBC
= ![]() sinαcosα+
sinαcosα+ ![]() sin2α
sin2α
= ![]() sin2α+
sin2α+ ![]() (1﹣cos2α)
(1﹣cos2α)
= ![]() (sin2α﹣cos2α)+
(sin2α﹣cos2α)+ ![]()
= ![]() sin(2α﹣
sin(2α﹣ ![]() )+
)+ ![]() ,
,
∵0<α< ![]() ,﹣
,﹣ ![]() <2α﹣
<2α﹣ ![]() <
< ![]() π,
π,
∴当2α﹣ ![]() =
= ![]() ,即α=
,即α= ![]() π时,S四边形ABTP最大
π时,S四边形ABTP最大
(2)解:|PA|+|PB|+|PC|=cosα+sinα+sinαcosα,
设t=cosα+sinα,则t2=cos2α+sin2α+2cosαsinα=1+2cosαsinα,
∴cosαsinα= ![]() ,
,
∴|PA|+|PB|+|PC|= ![]() +t=
+t= ![]() +t﹣
+t﹣ ![]() ,
,
∵t=cosα+sinα= ![]() sin(α+
sin(α+ ![]() )∈1,
)∈1, ![]() ],且t=﹣1(1,
],且t=﹣1(1, ![]() ],
],
∴|PA|+|PB|+|PC|= ![]() +t﹣
+t﹣ ![]() 在t∈(1,
在t∈(1, ![]() ]时单调递增,
]时单调递增,
则(|PA|+|PB|+|PC|)∈(1, ![]() +
+ ![]() ]
]
【解析】(1)由AB为圆的直径,利用圆周角定理得到∠APB为直角,再由AB=1,表示出PA与PB,根据PT与圆相切,表示出BC,进而表示出四边形ABTP的面积,整理后,利用正弦函数的值域及二次函数性质确定出最大值即可;(2)把表示出的PA,PB,PC代入所求式子,设t=cosα+sinα,可得出t2=1+2cosαsinα,进而表示出cosαsinα,代入所求式子整理为一个角的正弦函数,利用正弦函数的值域及二次函数性质确定出范围即可.


科目:高中数学 来源: 题型:
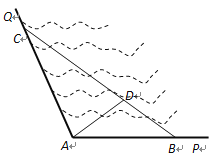
【题目】如图所示, ![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米, ![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接珠海作为全国文明城市的复查,爱卫会随机抽取了60位路人进行问卷调查,调查项目是自己对珠海各方面卫生情况的满意度(假设被问卷的路人回答是客观的),以分数表示问卷结果,并统计他们的问卷分数,把其中不低于50分的分成五段[50,60),[60,70),…[90,100]后画出如图部分频率分布直方图,观察图形信息,回答下列问题: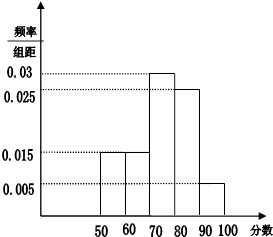
(1)求出问卷调查分数低于50分的被问卷人数;
(2)估计全市市民满意度在60分及以上的百分比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
(1)求A,(RA)∩B;
(2)若A∪C=R,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com