
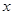 万元投资甲项目,
万元投资甲项目,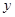 万元投资乙项目,试写出
万元投资乙项目,试写出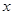 、
、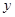 所满足的条件,并在直角坐标系内做出表示
所满足的条件,并在直角坐标系内做出表示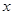 、
、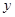 范围的图形;
范围的图形;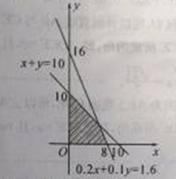 ;
;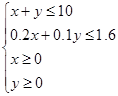 ,再在平面直角坐标系中画出对应的可行域,注意边界上的点也满足条件;(2)主要是利用可行域求解线性目标函数的最大值即得投资公司获得的最大利润,图解法解决含有实际背景的线性规划问题的基本步骤是:①列出约束条件,确定目标函数;②画出不等式(组)表示的平面区域;③作平行直线系使之与可行域有交点,求得最优解;④写出目标函数的最值,并下结论.
,再在平面直角坐标系中画出对应的可行域,注意边界上的点也满足条件;(2)主要是利用可行域求解线性目标函数的最大值即得投资公司获得的最大利润,图解法解决含有实际背景的线性规划问题的基本步骤是:①列出约束条件,确定目标函数;②画出不等式(组)表示的平面区域;③作平行直线系使之与可行域有交点,求得最优解;④写出目标函数的最值,并下结论.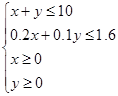 上述不等式组表示的平面区域如图中阴影部分(含边界),
上述不等式组表示的平面区域如图中阴影部分(含边界),
 ,作直线
,作直线 ,并作平行于直线
,并作平行于直线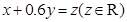 与可行域相交,当平行直线经过直线
与可行域相交,当平行直线经过直线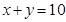 与
与 的交点
的交点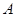 时,其截距最大,解方程组
时,其截距最大,解方程组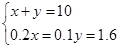 ,解得
,解得 ,即
,即 ,
,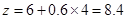 (万元),
(万元), 当
当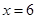 ,
,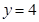 时,
时, 取得最大值.
取得最大值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:填空题
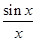 在点M(π,0)处的切线与两坐标轴围成的三角形区域为D(包含三角形内部与边界).若点P(x,y)是区域D内的任意一点,则x+4y的最大值为 .
在点M(π,0)处的切线与两坐标轴围成的三角形区域为D(包含三角形内部与边界).若点P(x,y)是区域D内的任意一点,则x+4y的最大值为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
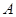 、
、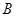 两类产品,甲种设备每天能生产
两类产品,甲种设备每天能生产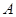 类产品
类产品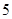 件和
件和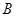 类产品
类产品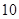 件,乙种设备每天能生产
件,乙种设备每天能生产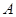 类产品
类产品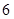 件和
件和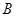 类产品
类产品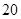 件.已知设备甲每天的租赁费为
件.已知设备甲每天的租赁费为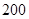 元,设备乙每天的租赁费为
元,设备乙每天的租赁费为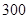 元,现该公司至少要生产
元,现该公司至少要生产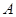 类产品
类产品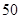 件,
件,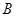 类产品
类产品 件,所需租赁费最少为____元.
件,所需租赁费最少为____元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com