
【题目】已知函数![]() .
.
(1)当![]() ,
,![]() 时,求满足
时,求满足![]() 的
的![]() 的值;
的值;
(2)若函数![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
①存在![]() ,使得不等式
,使得不等式![]() 有解,求实数
有解,求实数![]() 的取值范围;
的取值范围;
②若函数![]() 满足
满足![]() ,若对任意
,若对任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】分析:(1)把![]() ,
,![]() 代入
代入![]() ,求解即可得答案.
,求解即可得答案.
(2)①函数![]() 是定义在
是定义在![]() 上的奇函数,得
上的奇函数,得![]() ,代入原函数求解得
,代入原函数求解得![]() 的值,判断函数
的值,判断函数![]() 为单调性,由函数的单调性可得
为单调性,由函数的单调性可得![]() 的取值范围.
的取值范围.
②由![]() ,求得函数
,求得函数![]() ,代入
,代入![]() ,化简后得
,化简后得![]() 恒成立,令
恒成立,令![]() ,
,![]() ,参数分离得
,参数分离得![]() 在
在![]() 时恒成立,由基本不等即可求得
时恒成立,由基本不等即可求得![]() 的最大值.
的最大值.
详解:解:(1)因为![]() ,
,![]() ,所以
,所以![]() ,
,
化简得![]() ,解得
,解得![]() (舍)或
(舍)或![]() ,
,
所以![]() .
.
(2)因为![]() 是奇函数,所以
是奇函数,所以![]() ,所以
,所以![]() ,
,
化简变形得:![]() ,
,
要使上式对任意![]() 的成立,则
的成立,则![]() 且
且![]() ,
,
解得:![]() 或
或![]() ,因为
,因为![]() 的定义域是
的定义域是![]() ,所以
,所以![]() 舍去,
舍去,
所以![]() ,
,![]() ,所以
,所以![]() .
.
①![]()
对任意![]() ,
,![]() ,
,![]() 有:
有: ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因此![]() 在
在![]() 上递增,
上递增,
因为![]() ,所以
,所以![]() ,
,
即![]() 在
在![]() 时有解,
时有解,
当![]() 时,
时,![]() ,所以
,所以![]() .
.
②因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
不等式![]() 恒成立,即
恒成立,即![]() ,
,
令![]() ,
,![]() ,则
,则![]() 在
在![]() 时恒成立,
时恒成立,
因为![]() ,由基本不等式可得:
,由基本不等式可得:![]() ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
所以![]() ,则实数
,则实数![]() 的最大值为
的最大值为![]() .
.
|
| 转化不等式 |
奇函数 | 区间上单调递增 |
|
区间上单调递减 |
| |
偶函数 | 对称区间上左减右增 |
|
对称区间上左增右减 |
|


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
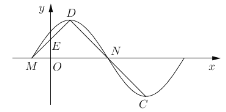
【题目】下图为函数![]() 的部分图象,
的部分图象,![]() 、
、![]() 是它与
是它与![]() 轴的两个交点,
轴的两个交点,![]() 、
、![]() 分别为它的最高点和最低点,
分别为它的最高点和最低点,![]() 是线段
是线段![]() 的中点,且
的中点,且![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求![]() 的解析式;
的解析式;
(2)将函数![]() 图象上的每个点的横坐标缩短为原来的一半,再向左平移
图象上的每个点的横坐标缩短为原来的一半,再向左平移![]() 个单位长度得到
个单位长度得到![]() 的图象,求
的图象,求![]() 的解析式及单调增区间,对称中心.
的解析式及单调增区间,对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学组织了地理知识竞赛,从参加考试的学生中抽出40名学生,将其成绩(均为整数)分成六组![]() ,
,![]() ,…,
,…,![]() ,其部分频率分布直方图如图所示.观察图形,回答下列问题.
,其部分频率分布直方图如图所示.观察图形,回答下列问题.

(1)求成绩在![]() 的频率,并补全这个频率分布直方图:
的频率,并补全这个频率分布直方图:
(2)估计这次考试的及格率(60分及以上为及格)和平均分;(计算时可以用组中值代替各组数据的平均值)
(3)从成绩在![]() 和
和![]() 的学生中选两人,求他们在同一分数段的概率.
的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在《周易》中,长横“![]() ”表示阳爻,两个短横“
”表示阳爻,两个短横“![]() ”表示阴爻.有放回地取阳爻和阴爻三次合成一卦,共有
”表示阴爻.有放回地取阳爻和阴爻三次合成一卦,共有![]() 种组合方法,这便是《系辞传》所说“太极生两仪,两仪生四象,四象生八卦”.有放回地取阳爻和阴爻一次有2种不同的情况,有放回地取阳爻和阴爻两次有四种情况,有放回地取阳爻和阴爻三次,八种情况.所谓的“算卦”,就是两个八卦的叠合,即共有放回地取阳爻和阴爻六次,得到六爻,然后对应不同的解析.在一次所谓“算卦”中得到六爻,这六爻恰好有三个阳爻三个阴爻的概率是( )
种组合方法,这便是《系辞传》所说“太极生两仪,两仪生四象,四象生八卦”.有放回地取阳爻和阴爻一次有2种不同的情况,有放回地取阳爻和阴爻两次有四种情况,有放回地取阳爻和阴爻三次,八种情况.所谓的“算卦”,就是两个八卦的叠合,即共有放回地取阳爻和阴爻六次,得到六爻,然后对应不同的解析.在一次所谓“算卦”中得到六爻,这六爻恰好有三个阳爻三个阴爻的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
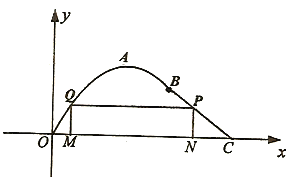
【题目】(本题16分)某乡镇为了进行美丽乡村建设,规划在长为10千米的河流OC的一侧建一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数![]() ,
,![]() (单位:千米)的图象,且曲线段的顶点为
(单位:千米)的图象,且曲线段的顶点为![]() ;观光带的后一部分为线段BC,如图所示.
;观光带的后一部分为线段BC,如图所示.
(1)求曲线段OABC对应的函数![]() 的解析式;
的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP, PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com