【答案】
分析:(1)根据所给的组合数的算式,把算式分解,约分整理,得到关于m的一元二次方程方程,解方程得到两个根,根据组合数的性质去掉不合题意的数字.
(2)把组合数分解,得到关于字母x的方程,是两个方程,解两个一元二次方程,得到四个结果,有两个结果不合题意,舍去.
(3)本题所给的一系列组合数的加法运算,遇到这种题目,一般考虑用组合数的性质,把前两项用组合数的性质,得到一个组合数,再把得到的结果和第三项用组合数的性质,以此类推,得到结果.
解答:解:(1)由已知得
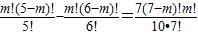
,
化简得m
2-23m+42=0,
解得m=2或21,
但0≤m≤5,故m=2.
∴
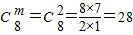
.
(2)原方程可化为x
2-x=5x-5或x
2-x=16-(5x-5),
即x
2-6x+5=0或x
2+4x-21=0,
解得x=1或x=5或x=-7或x=3,
经检验x=5或x=-7不合题意,
故原方程的根为x=1或x=3.
(3)原式=(C
11+C
111)+C
122+…+C
10099=(C
121+C
122)+…+C
10099
=(C
132+C
133)++C
10099=
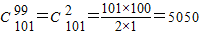
.
点评:本题是排列和组合数的运算,根据排列和组合的公式,写出算式,通过加减乘运算,得到结果,这类问题有一大部分是考查排列和组合的性质的,本题是一个简单的运算.

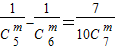 ,求C8m;
,求C8m;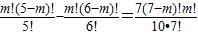 ,
,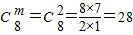 .
.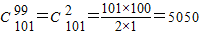 .
.
