
【题目】已知函数![]() ,
,![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;(2)求函数
处的切线方程;(2)求函数![]() 在
在![]() 上的最大值;
上的最大值;
(3)求证:存在唯一的![]() ,使得
,使得![]() .
.
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)是定义在R上的可导函数,其导函数为f′(x),当x>0时有2f(x)+xf′(x)>x2 , 则不等式(x+2014)2f(x+2014)+4f(﹣2)<0的解集为( )
A.(﹣∞,﹣2012)
B.(﹣2016,﹣2012)
C.(﹣∞,﹣2016)
D.(﹣2016,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.若在通道的分叉处,小弹子以相同的概率落入每个通道,记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).某研究性学习小组经探究发现小弹子落入第n层的第m个通道的次数服从二项分布,请你解决下列问题.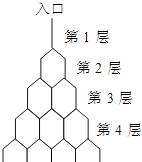
(1)求P(2,1),P(3,2)及P(4,2)的值,并猜想P(n,m)的表达式.(不必证明)
(2)设小弹子落入第6层第m个竖直通道得到分数为ξ,其中ξ= ![]() ,试求ξ的分布列及数学期望.
,试求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0,其中a<0,q:实数x满足x2﹣x﹣6≤0或x2+2x﹣8>0,且非p是非q的必要不充分条件,则实数a的范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某刻考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差![]() (单位:分)与物理偏差
(单位:分)与物理偏差![]() (单位:分)之间的关系进行偏差分析,决定从全班40位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如表:
(单位:分)之间的关系进行偏差分析,决定从全班40位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如表:

(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若这次考试该班数学平均分为120分,物理平均分为92,试预测数学成绩126分的同学的物理成绩.
参考公式:  ,
, ![]()
参考数据: ![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的函数 ![]() .
.
(1)如果函数 ![]() ,求b、c;
,求b、c;
(2)设当x∈( ![]() ,3)时,函数y=f(x)﹣c(x+b)的图象上任一点P处的切线斜率为k,若k≤2,求实数b的取值范围.
,3)时,函数y=f(x)﹣c(x+b)的图象上任一点P处的切线斜率为k,若k≤2,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.
(1)求实数![]() ,
, ![]() 的值;
的值;
(2)是否存在实数![]() ,当
,当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,若存在,求出
,若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)若![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com