
【题目】在直角坐标系xOy中,直线l的参数方程为 ![]() (t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位.且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=6sinθ.
(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位.且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=6sinθ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(1,2),求|PA|+|PB|的最小值.
【答案】
(1)解:由ρ=6sinθ得ρ2=6ρsinθ,
化为直角坐标方程为x2+y2=6y,即x2+(y﹣3)2=9.
(2)解:将l的参数方程代入圆C的直角坐标方程,得t2+2(cosα﹣sinα)t﹣7=0.
由△=(2cosα﹣2sinα)2+4×7>0,故可设t1,t2是上述方程的两根,
所以 ![]() 又直线l过点(1,2),
又直线l过点(1,2),
故结合t的几何意义得|PA|+|PB|= ![]() =
= ![]() .
.
所以|PA|+|PB|的最小值为 ![]() .
.
【解析】(1)利用x=ρcosθ,y=ρsinθ可将圆C极坐标方程化为直角坐标方程;(2)先根据(1)得出圆C的普通方程,再根据直线与交与交于A,B两点,可以把直线与曲线联立方程,用根与系数关系结合直线参数方程的几何意义,表示出|PA|+|PB|,最后根据三角函数的性质,即可得到求解最小值.
【考点精析】根据题目的已知条件,利用圆的标准方程的相关知识可以得到问题的答案,需要掌握圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程.
;圆心为A(a,b),半径为r的圆的方程.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对新研发的一种产品进行试销,得到如下数据表:
(1)根据上表求出回归直线方程 ![]() ,并预测当单价定为8.3元时的销量;
,并预测当单价定为8.3元时的销量;
(2)如果该工厂每件产品的成本为5.5元,利用所求的回归方程,要使得利润最大,单价应该定为多少?
附:线性回归方程 ![]() 中斜率和截距最小二乘估计计算公式:
中斜率和截距最小二乘估计计算公式: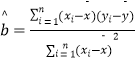 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1的圆心在坐标原点O,且恰好与直线![]() 相切.
相切.
(Ⅰ)求圆C1的标准方程;
(Ⅱ)设点A为圆上一动点,AN垂直于x轴于点N,若动点Q满足![]()
(其中m为非零常数),试求动点Q的轨迹方程;
(Ⅲ)在(Ⅱ)的结论下,当m=![]() 时,得到动点Q的轨迹为曲线C,与l1垂直的直线l与曲线C交于B,D两点,求△OBD面积的最大值.
时,得到动点Q的轨迹为曲线C,与l1垂直的直线l与曲线C交于B,D两点,求△OBD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机调查询问110名性别不同的高中生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() 计算得
计算得 ![]()
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C.有99%以上的把握认为“爱好该项运动与性别无关”
D.有99%以上的把握认为“爱好该项运动与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①若 ![]() ,则
,则 ![]() 或
或 ![]() ;
;
② ![]() ,都有
,都有 ![]() ;
;
③若 ![]() 是实数,则
是实数,则 ![]() 是
是 ![]() 的充分不必要条件;
的充分不必要条件;
④“ ![]() ” 的否定是“
” 的否定是“ ![]() ” ;
” ;
其中真命题的个数是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标中,直线l的方程为 ![]() ,曲线C的方程为
,曲线C的方程为 ![]() .
.
(1)求直线l与极轴的交点到极点的距离;
(2)若曲线C上恰好有两个点到直线l的距离为 ![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() ,
,![]() ,且
,且![]() (n=1,2,...).记
(n=1,2,...).记
集合![]() .
.
(1)(Ⅰ)若![]() ,写出集合M的所有元素;
,写出集合M的所有元素;
(2)(Ⅱ)若集合M存在一个元素是3的倍数,证明:M的所有元素都是3的倍数;
(3)(Ⅲ)求集合M的元素个数的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com