
【题目】已知集合![]() …,
…,![]() …,
…,![]() ,对于
,对于![]() …,
…,![]() ,B=(
,B=(![]() …,
…,![]() ,定义A与B的差为
,定义A与B的差为
![]() …
…![]() ,A与B之间的距离为
,A与B之间的距离为![]() .
.
(Ⅰ)若![]() ,求
,求![]() ;
;
(Ⅱ)证明:对任意![]() ,有
,有
(i)![]() ,且
,且![]() ;
;
(ii)![]() 三个数中至少有一个是偶数;
三个数中至少有一个是偶数;
(Ⅲ)对于![]() …
…![]() …
…![]() ,再定义一种A与B之间的运算,并写出两条该运算满足的性质(不需证明).
,再定义一种A与B之间的运算,并写出两条该运算满足的性质(不需证明).
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】分析:(Ⅰ)因为![]() ,所以
,所以![]() ;(Ⅱ)(i)设
;(Ⅱ)(i)设![]() …
…![]() …
…![]() …
…![]() ,因为
,因为![]() ,故
,故![]() ,…,n),分两种情况讨论即可的结果;(ii)设
,…,n),分两种情况讨论即可的结果;(ii)设![]() …,
…,![]() …,
…,![]() …
…![]() ,记
,记![]()
记![]() …
…![]() ,由(i)可知
,由(i)可知![]() ,
,![]() ,
,![]() ,
,
即![]() …
…![]() ,先推导出
,先推导出![]() 不可能全为奇数,即
不可能全为奇数,即![]() 三个数中至少有一个是偶数,从而可得结论;(Ⅲ)定义
三个数中至少有一个是偶数,从而可得结论;(Ⅲ)定义![]() =
=![]() ,…
,…![]() ,则
,则![]() .
.
详解:(Ⅰ)因为![]() ,所以
,所以![]() .
.
(Ⅱ)(i)设![]() …
…![]() …
…![]() …
…![]() ,
,
因为![]() ,故
,故![]() ,…,n),
,…,n),
即![]() …
…![]() .
.
又![]() …,n.
…,n.
当![]() 时,有
时,有![]() ;
;
当![]() 时,有
时,有![]() ;
;
故![]()
(ii)设![]() …,
…,![]() …,
…,![]() …
…![]() ,
,
记![]()
记![]() …
…![]() ,由(i)可知:
,由(i)可知:
![]() ,
,
![]() ,
,
![]() ,
,
即![]() 中1的个数为k,
中1的个数为k,![]() 中1的个数为
中1的个数为![]() ,…
,…![]()
设t是使![]() 成立的i的个数,则有
成立的i的个数,则有![]() ,
,
由此可知,![]() 不可能全为奇数,即
不可能全为奇数,即![]() 三个数中至少有一个是偶数.
三个数中至少有一个是偶数.
(Ⅲ)如可定义A·B=![]() ,…
,…![]() ,则A·B=B·A,(A·B)·C=A·(B·C).
,则A·B=B·A,(A·B)·C=A·(B·C).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,![]() 是东西方向的公路北侧的边缘线,某公司准备在
是东西方向的公路北侧的边缘线,某公司准备在![]() 上的一点
上的一点![]() 的正北方向的
的正北方向的![]() 处建一仓库,并在公路同侧建造一个正方形无顶中转站
处建一仓库,并在公路同侧建造一个正方形无顶中转站![]() (其中边
(其中边![]() 在
在![]() 上),现从仓库
上),现从仓库![]() 向
向![]() 和中转站分别修两条道路
和中转站分别修两条道路![]() ,
,![]() ,已知
,已知![]() ,且
,且![]() ,设
,设![]() ,
,![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)如果中转站四周围墙(即正方形周长)造价为![]() 万元
万元![]() ,两条道路造价为
,两条道路造价为![]() 万元
万元![]() ,问:
,问:![]() 取何值时,该公司建中转围墙和两条道路总造价
取何值时,该公司建中转围墙和两条道路总造价![]() 最低?
最低?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
A.月接待游客逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两艘轮船都要停靠在同一个泊位,它们可能在一昼夜的任意时刻到达.甲、乙两船停靠泊位的时间分别为4小时与2小时,求有一艘船停靠泊位时必需等待一段时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆 ![]() 的方程为
的方程为 ![]() ,直线
,直线 ![]() 的方程为
的方程为 ![]() ,点
,点 ![]() 在直线
在直线 ![]() 上,过点
上,过点 ![]() 作圆
作圆 ![]() 的切线
的切线 ![]() ,切点为
,切点为 ![]() .
.
(1)若点 ![]() 的坐标为
的坐标为 ![]() ,求切线
,求切线 ![]() 的方程;
的方程;
(2)求四边形 ![]() 面积的最小值;
面积的最小值;
(3)求证:经过 ![]() 三点的圆必过定点,并求出所有定点坐标.
三点的圆必过定点,并求出所有定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分别求适合下列条件的椭圆的标准方程.
(1)焦点在坐标轴上,且经过点A ( ![]() ,-2),B(-2
,-2),B(-2 ![]() ,1);
,1);
(2)与椭圆 ![]() 有相同焦点且经过点M(
有相同焦点且经过点M( ![]() ,1).
,1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经营某种商品,在某周内获纯利![]() (元)与该周每天销售这种商品数
(元)与该周每天销售这种商品数![]() 之间的一组数据关系如表:
之间的一组数据关系如表:
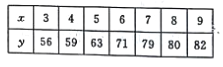
(I)画出散点图;
(II)求纯利![]() 与每天销售件数
与每天销售件数![]() 之间的回归直线方程;
之间的回归直线方程;
(III)估计当每天销售的件数为12件时,每周内获得的纯利为多少?
附注:
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题 ![]() “存在
“存在 ![]() ”,命题
”,命题 ![]() :“曲线
:“曲线 ![]() 表示焦点在
表示焦点在 ![]() 轴上的椭圆”,命题
轴上的椭圆”,命题 ![]() “曲线
“曲线 ![]() 表示双曲线”
表示双曲线”
(1)若“ ![]() 且
且 ![]() ”是真命题,求实数
”是真命题,求实数 ![]() 的取值范围;
的取值范围;
(2)若 ![]() 是
是 ![]() 的必要不充分条件,求实数
的必要不充分条件,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com