
【题目】已知直线l的参数方程为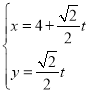 (t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(t为参数),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.
(1)求圆C的直角坐标方程及弦AB的长;
(2)动点P在圆C上(不与A,B重合),试求△ABP的面积的最大值.
【答案】(1)(x-2)2+y2=4;![]() ;(2)2+
;(2)2+![]() .
.
【解析】
(1)圆C的极坐标方程化为直角坐标方程,直线l的参数方程代入圆C的的直角坐标方程,利用直线参数方程的几何意义,即可求解;
(2)要求△ABP的面积的最大值,只需求出点P到直线l距离的最大值,将点P坐标设为圆方程的参数形式,利用点到直线的距离公式以及三角函数的有界性,即可求解.
(1)由ρ=4cos θ得ρ2=4ρcos θ,所以x2+y2-4x=0,
所以圆C的直角坐标方程为(x-2)2+y2=4.
设A,B对应的参数分别为t1,t2.
将直线l的参数方程代入圆C:
(x-2)2+y2=4,并整理得t2+![]() t=0,
t=0,
解得t1=0,t2=-![]() .
.
所以直线l被圆C截得的弦AB的长为|t1-t2|=![]() .
.
(2)由题意得,直线l的普通方程为x-y-4=0.
圆C的参数方程为![]() (θ为参数),
(θ为参数),
可设圆C上的动点P(2+2cos θ,2sin θ),
则点P到直线l的距离
d=![]() ,
,
当![]() =-1时,d取得最大值,且d的最大值为2+
=-1时,d取得最大值,且d的最大值为2+![]() .
.
所以S△ABP=![]() ×
×![]() ×(2+
×(2+![]() )=2+
)=2+![]() ,
,
即△ABP的面积的最大值为2+![]() .
.


科目:高中数学 来源: 题型:
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气 日落云里走 | 下雨 | 未下雨 |
出现 | 25 | 5 |
未出现 | 25 | 45 |
临界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并计算得到![]() ,下列小波对地区A天气判断不正确的是( )
,下列小波对地区A天气判断不正确的是( )
A.夜晚下雨的概率约为![]()
B.未出现“日落云里走”夜晚下雨的概率约为![]()
C.有![]() 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有![]() 的把握认为夜晚会下雨
的把握认为夜晚会下雨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开为了了解哪些人更关注“两会”,某机构随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制的频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”经统计“青少年人”和“中老年人”的人数之比为
内的人分别称为“青少年人”和“中老年人”经统计“青少年人”和“中老年人”的人数之比为![]() .其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是
.其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是![]() .
.

(1)求图中![]() 的值;现釆用分层抽样在
的值;现釆用分层抽样在![]() 和
和![]() 中随机抽取8名代表,从8人中仼选2人,求2人中至少有1个是“中老年人”的概率是多少?
中随机抽取8名代表,从8人中仼选2人,求2人中至少有1个是“中老年人”的概率是多少?
(2)根据已知条件,完成下面的![]() 列联表,并根据此统计结果判断:能否有
列联表,并根据此统计结果判断:能否有![]() 的把握认为“中老年人”比“青少年人”更加关注“两会”?
的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
参考数据及公式:
| 0.150 | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axlnx﹣x2﹣ax+1(a∈R)在定义域内有两个不同的极值点.
(1)求实数a的取值范围;
(2)设两个极值点分别为x1,x2,x1<x2,证明:f(x1)+f(x2)<2﹣x12+x22.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com