
ЁОЬтФПЁП2019ФъШЋЙњЁАСНЛсЁБЃЌМДжаЛЊШЫУёЙВКЭЙњЕкЪЎШ§НьШЋЙњШЫДѓЖўДЮЛсвщКЭжаЙњШЫУёеўжЮаЩЬЛсвщЕкЪЎШ§НьШЋЙњЮЏдБЛсЕкЖўДЮЛсвщЃЌЗжБ№гк2019Фъ3дТ5ШеКЭ3дТ3ШедкББОЉейПЊЮЊСЫСЫНтФФаЉШЫИќЙизЂЁАСНЛсЁБЃЌФГЛњЙЙЫцЛњГщШЁСЫФъСфдк15~75ЫъжЎМфЕФ200ШЫНјааЕїВщЃЌВЂАДФъСфЛцжЦЕФЦЕТЪЗжВМжБЗНЭМШчЭМЫљЪОЃЌАбФъСфТфдкЧјМф![]() КЭ
КЭ![]() ФкЕФШЫЗжБ№ГЦЮЊЁАЧрЩйФъШЫЁБКЭЁАжаРЯФъШЫЁБОЭГМЦЁАЧрЩйФъШЫЁБКЭЁАжаРЯФъШЫЁБЕФШЫЪ§жЎБШЮЊ
ФкЕФШЫЗжБ№ГЦЮЊЁАЧрЩйФъШЫЁБКЭЁАжаРЯФъШЫЁБОЭГМЦЁАЧрЩйФъШЫЁБКЭЁАжаРЯФъШЫЁБЕФШЫЪ§жЎБШЮЊ![]() .ЦфжаЁАЧрЩйФъШЫЁБжага40ШЫЙизЂЁАСНЛсЁБЃЌЁАжаРЯФъШЫЁБжаЙизЂЁАСНЛсЁБКЭВЛЙизЂЁАСНЛсЁБЕФШЫЪ§жЎБШЪЧ
.ЦфжаЁАЧрЩйФъШЫЁБжага40ШЫЙизЂЁАСНЛсЁБЃЌЁАжаРЯФъШЫЁБжаЙизЂЁАСНЛсЁБКЭВЛЙизЂЁАСНЛсЁБЕФШЫЪ§жЎБШЪЧ![]() .
.

ЃЈ1ЃЉЧѓЭМжа![]() ЕФжЕЃЛЯжсгУЗжВуГщбљдк
ЕФжЕЃЛЯжсгУЗжВуГщбљдк![]() КЭ
КЭ![]() жаЫцЛњГщШЁ8УћДњБэЃЌДг8ШЫжаЉбЁ2ШЫЃЌЧѓ2ШЫжажСЩйга1ИіЪЧЁАжаРЯФъШЫЁБЕФИХТЪЪЧЖрЩйЃП
жаЫцЛњГщШЁ8УћДњБэЃЌДг8ШЫжаЉбЁ2ШЫЃЌЧѓ2ШЫжажСЩйга1ИіЪЧЁАжаРЯФъШЫЁБЕФИХТЪЪЧЖрЩйЃП
ЃЈ2ЃЉИљОнвбжЊЬѕМўЃЌЭъГЩЯТУцЕФ![]() СаСЊБэЃЌВЂИљОнДЫЭГМЦНсЙћХаЖЯЃКФмЗёга
СаСЊБэЃЌВЂИљОнДЫЭГМЦНсЙћХаЖЯЃКФмЗёга![]() ЕФАбЮеШЯЮЊЁАжаРЯФъШЫЁББШЁАЧрЩйФъШЫЁБИќМгЙизЂЁАСНЛсЁБЃП
ЕФАбЮеШЯЮЊЁАжаРЯФъШЫЁББШЁАЧрЩйФъШЫЁБИќМгЙизЂЁАСНЛсЁБЃП
ЙизЂ | ВЛЙизЂ | КЯМЦ | |
ЧрЩйФъШЫ | |||
жаРЯФъШЫ | |||
КЯМЦ |
ВЮПМЪ§ОнМАЙЋЪНЃК
| 0.150 | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |

ЁОД№АИЁП(1)![]() ЃЛ
ЃЛ![]() ЃЛ(2)БэИёМћЯъНтЃЛга
ЃЛ(2)БэИёМћЯъНтЃЛга![]() ЕФАбЮеШЯЮЊЁАжаРЯФъШЫЁББШЁАЧрЩйФъШЫЁБИќМгЙизЂЁАСНЛсЁБ.
ЕФАбЮеШЯЮЊЁАжаРЯФъШЫЁББШЁАЧрЩйФъШЫЁБИќМгЙизЂЁАСНЛсЁБ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЬѕМўЃЌНсКЯЦЕТЪЗжВМжБЗНЭМЃЌМДПЩШнвзЧѓЕУВЮЪ§![]() ЃЛРћгУЗжВуГщбљЕФЕШБШР§ГщШЁЕФЬиЕуЃЌЧѓГіИїЧјМфГщШЁЕФШЫЪ§ЃЌдйЧѓЙХЕфИХаЭЕФИХТЪМДПЩЃЛ
ЃЛРћгУЗжВуГщбљЕФЕШБШР§ГщШЁЕФЬиЕуЃЌЧѓГіИїЧјМфГщШЁЕФШЫЪ§ЃЌдйЧѓЙХЕфИХаЭЕФИХТЪМДПЩЃЛ
ЃЈ2ЃЉЯШВЙГфЭъГЩБэИёЃЌдйМЦЫу![]() ЃЌОнДЫХаЖЯ.
ЃЌОнДЫХаЖЯ.
ЃЈ1ЃЉИљОнЬтвтПЩжЊЃЌТфдкЧјМф![]() ЕФШЫЪ§ЮЊ
ЕФШЫЪ§ЮЊ![]() ШЫЃЌ
ШЫЃЌ
ТфдкЧјМф![]() ЕФШЫЪ§ЮЊ
ЕФШЫЪ§ЮЊ![]() ШЫЃЛ
ШЫЃЛ
ЙЪПЩЕУ![]() ЃЌ
ЃЌ
![]()
НтЕУ![]() ЃЛ
ЃЛ
гжТфдк![]() КЭ
КЭ![]() жаЕФШЫЪ§ЗжБ№ЮЊ
жаЕФШЫЪ§ЗжБ№ЮЊ![]() ШЫЃЌ
ШЫЃЌ
ИљОнЗжВуГщбљЕШБШР§ГщШЁЕФаджЪЃЌ
ДгвдЩЯСНзщжагІИУЗжБ№ГщШЁЕФШЫЪ§ЮЊ![]() ШЫ.
ШЫ.
дђ2ШЫжажСЩйга1ИіЪЧЁАжаРЯФъШЫЁБЕФИХТЪ![]() .
.
ЃЈ2ЃЉИљОнЬтвтВЙГфБэИёШчЯТЃК
ЙизЂ | ВЛЙизЂ | КЯМЦ | |
ЧрЩйФъШЫ | 40 | 55 | 95 |
жаРЯФъШЫ | 70 | 35 | 105 |
КЯМЦ | 110 | 90 | 200 |
ЙЪ![]() .
.
ЙЪга![]() ЕФАбЮеШЯЮЊЁАжаРЯФъШЫЁББШЁАЧрЩйФъШЫЁБИќМгЙизЂЁАСНЛсЁБ.
ЕФАбЮеШЯЮЊЁАжаРЯФъШЫЁББШЁАЧрЩйФъШЫЁБИќМгЙизЂЁАСНЛсЁБ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇ![]() ЃЌ
ЃЌ![]() СНЬѕЯрЛЅЖРСЂЕФЩњВњЯпЩњВњЭЌПюВњЦЗЃЌдкВњСПвЛбљЕФЧщПіЯТЃЌЭЈЙ§ШеГЃМрПиЕУжЊЃЌ
СНЬѕЯрЛЅЖРСЂЕФЩњВњЯпЩњВњЭЌПюВњЦЗЃЌдкВњСПвЛбљЕФЧщПіЯТЃЌЭЈЙ§ШеГЃМрПиЕУжЊЃЌ![]() ЃЌ
ЃЌ![]() ЩњВњЯпЩњВњЕФВњЦЗЮЊКЯИёЦЗЕФИХТЪЗжБ№ЮЊ
ЩњВњЯпЩњВњЕФВњЦЗЮЊКЯИёЦЗЕФИХТЪЗжБ№ЮЊ![]() КЭ
КЭ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉДг![]() ЃЌ
ЃЌ![]() ЩњВњЯпЩЯИїГщМьвЛМўВњЦЗЃЌШєЪЙЕУВњЦЗжСЩйгавЛМўКЯИёЕФИХТЪВЛЕЭгк99.5%ЃЌЧѓ
ЩњВњЯпЩЯИїГщМьвЛМўВњЦЗЃЌШєЪЙЕУВњЦЗжСЩйгавЛМўКЯИёЕФИХТЪВЛЕЭгк99.5%ЃЌЧѓ![]() ЕФзюаЁжЕ
ЕФзюаЁжЕ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉМйЩшВЛКЯИёЕФВњЦЗОљПЩНјааЗЕЙЄаоИДЮЊКЯИёЦЗЃЌвдЃЈ1ЃЉжаШЗЖЈЕФ![]() зїЮЊ
зїЮЊ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЂйвбжЊ![]() ЃЌ
ЃЌ![]() ЩњВњЯпЕФВЛКЯИёЦЗЗЕЙЄКѓУПМўВњЦЗПЩЗжБ№ЭьЛиЫ№ЪЇ5дЊКЭ3дЊЃЌШєДгСНЬѕЩњВњЯпЩЯИїЫцЛњГщМь1000МўВњЦЗЃЌвдЭьЛиЫ№ЪЇЕФЦНОљЪ§ЮЊХаЖЯвРОнЃЌЙРМЦФФЬѕЩњВњЯпЕФЭьЛиЫ№ЪЇНЯЖрЃП
ЩњВњЯпЕФВЛКЯИёЦЗЗЕЙЄКѓУПМўВњЦЗПЩЗжБ№ЭьЛиЫ№ЪЇ5дЊКЭ3дЊЃЌШєДгСНЬѕЩњВњЯпЩЯИїЫцЛњГщМь1000МўВњЦЗЃЌвдЭьЛиЫ№ЪЇЕФЦНОљЪ§ЮЊХаЖЯвРОнЃЌЙРМЦФФЬѕЩњВњЯпЕФЭьЛиЫ№ЪЇНЯЖрЃП
ЂкШєзюжеЕФКЯИёЦЗЃЈАќРЈЗЕЙЄаоИДКѓЕФКЯИёЦЗЃЉАДеевЛЁЂЖўЁЂШ§ЕШМЖЗжРрКѓЃЌУПМўПЩЗжБ№ЛёРћ10дЊЁЂ8дЊЁЂ6дЊЃЌЯжДг![]() ЃЌ
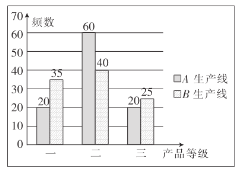
ЃЌ![]() ЩњВњЯпЕФзюжеКЯИёЦЗжаИїЫцЛњГщШЁ100МўНјааЗжМЖМьВтЃЌНсЙћЭГМЦШчЭМЫљЪОЃЌгУбљБОЕФЦЕТЪЗжВМЙРМЦзмЬхЗжВМЃЌМЧИУЙЄГЇЩњВњвЛМўВњЦЗЕФРћШѓЮЊ
ЩњВњЯпЕФзюжеКЯИёЦЗжаИїЫцЛњГщШЁ100МўНјааЗжМЖМьВтЃЌНсЙћЭГМЦШчЭМЫљЪОЃЌгУбљБОЕФЦЕТЪЗжВМЙРМЦзмЬхЗжВМЃЌМЧИУЙЄГЇЩњВњвЛМўВњЦЗЕФРћШѓЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаВЂЙРМЦИУГЇВњСП2000МўЪБРћШѓЕФЦкЭћжЕЃЎ
ЕФЗжВМСаВЂЙРМЦИУГЇВњСП2000МўЪБРћШѓЕФЦкЭћжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
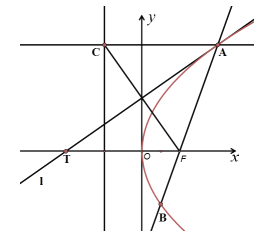
ЁОЬтФПЁПвбжЊЯпЖЮ![]() ЪЧЙ§ХзЮяЯп
ЪЧЙ§ХзЮяЯп![]() ЕФНЙЕуFЕФвЛЬѕЯвЃЌЙ§ЕуAЃЈAдкЕквЛЯѓЯоФкЃЉзїжБЯп
ЕФНЙЕуFЕФвЛЬѕЯвЃЌЙ§ЕуAЃЈAдкЕквЛЯѓЯоФкЃЉзїжБЯп![]() ДЙжБгкХзЮяЯпЕФзМЯпЃЌДЙзуЮЊCЃЌжБЯп
ДЙжБгкХзЮяЯпЕФзМЯпЃЌДЙзуЮЊCЃЌжБЯп![]() гыХзЮяЯпЯрЧагкЕуAЃЌНЛxжсгкЕуTЃЌИјГіЯТСаУќЬтЃК
гыХзЮяЯпЯрЧагкЕуAЃЌНЛxжсгкЕуTЃЌИјГіЯТСаУќЬтЃК
ЃЈ1ЃЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉ![]() .
.
Цфжае§ШЗЕФУќЬтИіЪ§ЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпlЕФВЮЪ§ЗНГЬЮЊ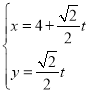 (tЮЊВЮЪ§)ЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФЗЧИКАыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌдВCЕФМЋзјБъЗНГЬЮЊІбЃН4cos ІШЃЌжБЯпlгыдВCНЛгкAЃЌBСНЕуЃЎ
(tЮЊВЮЪ§)ЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФЗЧИКАыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌдВCЕФМЋзјБъЗНГЬЮЊІбЃН4cos ІШЃЌжБЯпlгыдВCНЛгкAЃЌBСНЕуЃЎ
(1)ЧѓдВCЕФжБНЧзјБъЗНГЬМАЯвABЕФГЄЃЛ
(2)ЖЏЕуPдкдВCЩЯ(ВЛгыAЃЌBжиКЯ)ЃЌЪдЧѓЁїABPЕФУцЛ§ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаЮхИіУќЬтЃК
ЂйвбжЊжБЯп![]() ЁЂ
ЁЂ![]() КЭЦНУц
КЭЦНУц![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
ЂкЦНУцЩЯЕНвЛИіЖЈЕуКЭвЛЬѕЖЈжБЯпЕФОрРыЯрЕШЕФЕуЕФЙьМЃЪЧвЛЬѕХзЮяЯпЃЛ
ЂлЫЋЧњЯп![]() ЃЌдђжБЯп
ЃЌдђжБЯп![]()
![]() гыЫЋЧњЯпгаЧвжЛгавЛИіЙЋЙВЕуЃЛ
гыЫЋЧњЯпгаЧвжЛгавЛИіЙЋЙВЕуЃЛ
ЂмШєСНИіЦНУцДЙжБЃЌФЧУДвЛИіЦНУцФкгыЫќУЧЕФНЛЯпВЛДЙжБЕФжБЯпгыСэвЛИіЦНУцвВВЛДЙжБЃЛ
ЂнЙ§![]() ЕФжБЯп
ЕФжБЯп![]() гыЭждВ
гыЭждВ![]() НЛгк
НЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЯпЖЮ
СНЕуЃЌЯпЖЮ![]() жаЕуЮЊ
жаЕуЮЊ![]() ЃЌЩшжБЯп
ЃЌЩшжБЯп![]() аБТЪЮЊ
аБТЪЮЊ![]()
![]() ЃЌжБЯп
ЃЌжБЯп![]() ЕФаБТЪЮЊ
ЕФаБТЪЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕШгк
ЕШгк![]() .
.
ЦфжаЃЌе§ШЗУќЬтЕФађКХЮЊ_______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЙсГЙжаЙВжабыЙњЮёдКЙигкОЋзМЗіЦЖеўВпЕФЙ§ГЬжаЃЌФГЕЅЮЛЖЈЕуАяЗі100ЛЇЦЖРЇЛЇ.ЙЄзїзщЖдет100ЛЇДхУёЕФЦЖРЇзДПіКЭМвЭЅГЩдБЪмНЬг§ЧщПіНјааСЫЕїВщЃКМзДх55ЛЇЦЖРЇДхУёжаЃЌМвЭЅГЩдБНгЪмЙ§жаЕШМАвдЩЯНЬг§ЕФжЛга10ЛЇЃЌввДх45ЛЇЦЖРЇДхУёжаЃЌМвЭЅГЩдБНгЪмЙ§жаЕШМАвдЩЯНЬг§ЕФга20ЛЇ.
ЃЈ1ЃЉЭъГЩЯТУцЕФСаСЊБэЃЌВЂХаЖЯЪЧЗёга99.5%ЕФАбЮеШЯЮЊЦЖРЇгыНгЪмНЬг§ЧщПігаЙиЃЛ
МвЭЅГЩдБНгЪмЙ§жаЕШвдЯТ НЬг§ЕФЛЇЪ§ | МвЭЅГЩдБНгЪмЙ§жаЕШМАвдЩЯ НЬг§ЕФЛЇЪ§ | КЯМЦ | |
МзДхЦЖРЇЛЇЪ§ | |||
ввДхЦЖРЇЛЇЪ§ | |||
КЯМЦ |
ЃЈ2ЃЉдкБЛАяЗіЕФ100ЛЇЦЖРЇЛЇжаЃЌАДЗжВуГщбљЕФЗНЗЈДгМвЭЅГЩдБНгЪмЙ§жаЕШМАвдЩЯНЬг§ЕФЦЖРЇЛЇжаГщШЁ6ЛЇЃЌдйДгет6ЛЇжаВЩгУМђЕЅЫцЛњГщбљЕФЗНЗЈЫцЛњГщШЁ2ЛЇЃЌЧѓет2ЛЇжаМзЁЂввСНДхЧЁКУИї1ЛЇЕФИХТЪ.
ВЮПМЙЋЪНгыЪ§ОнЃК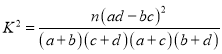 ЃЌЦфжа
ЃЌЦфжа![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
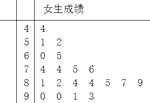
ЁОЬтФПЁПЮЊСЫбаОПФГбЇПЦГЩМЈЪЧЗёгыбЇЩњадБ№гаЙиЃЌВЩгУЗжВуГщбљЕФЗНЗЈЃЌДгИпШ§ФъМЖГщШЁСЫ30УћФаЩњКЭ20УћХЎЩњЕФИУбЇПЦГЩМЈЃЌЕУЕНШчЯТЫљЪОФаЩњГЩМЈЕФЦЕТЪЗжВМжБЗНЭМКЭХЎЩњГЩМЈЕФОЅвЖЭМЃЌЙцЖЈ80ЗжвдЩЯЮЊгХЗжЃЈКЌ80ЗжЃЉЃЎ

ЃЈЂёЃЉЃЈiЃЉЧыИљОнЭМЪОЃЌНЋ2ЁС2СаСЊБэВЙГфЭъећЃЛ
гХЗж | ЗЧгХЗж | змМЦ | |
ФаЩњ | |||
ХЎЩњ | |||
змМЦ | 50 |
ЃЈiiЃЉОнДЫСаСЊБэХаЖЯЃЌФмЗёдкЗИДэЮѓИХТЪВЛГЌЙ§10%ЕФЧАЬсЯТШЯЮЊЁАИУбЇПЦГЩМЈгыадБ№гаЙиЁБЃП
ЃЈЂђЃЉНЋЦЕТЪЪгзїИХТЪЃЌДгИпШ§ФъМЖИУбЇПЦГЩМЈжаШЮвтГщШЁ3УћбЇЩњЕФГЩМЈЃЌЧѓжСЩй2УћбЇЩњЕФГЩМЈЮЊгХЗжЕФИХТЪЃЎ
ИНЃК
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќЮхФъРДФГВнГЁбђжЛЪ§СПгыВнГЁжВБЛжИЪ§СНБфСПМфЕФЙиЯЕШчБэЫљЪОЃЌЛцжЦЯргІЕФЩЂЕуЭМЃЌШчЭМЫљЪОЃК
ФъЗн | 1 | 2 | 3 | 4 | 5 |
бђжЛЪ§СПЃЈЭђжЛЃЉ | 1.4 | 0.9 | 0.75 | 0.6 | 0.3 |
ВнЕижВБЛжИЪ§ | 1.1 | 4.3 | 15.6 | 31.3 | 49.7 |

ИљОнБэМАЭМЕУЕНвдЯТХаЖЯЃКЂйбђжЛЪ§СПгыВнГЁжВБЛжИЪ§ГЩМѕКЏЪ§ЙиЯЕЃЛЂкШєРћгУетЮхзщЪ§ОнЕУЕНЕФСНБфСПМфЕФЯрЙиЯЕЪ§ЮЊ![]() ЃЌШЅЕєЕквЛФъЪ§ОнКѓЕУЕНЕФЯрЙиЯЕЪ§ЮЊ
ЃЌШЅЕєЕквЛФъЪ§ОнКѓЕУЕНЕФЯрЙиЯЕЪ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЛЂлПЩвдРћгУЛиЙщжБЯпЗНГЬЃЌзМШЗЕиЕУЕНЕБбђжЛЪ§СПЮЊ2ЭђжЛЪБЕФВнГЁжВБЛжИЪ§ЃЛвдЩЯХаЖЯжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
ЃЛЂлПЩвдРћгУЛиЙщжБЯпЗНГЬЃЌзМШЗЕиЕУЕНЕБбђжЛЪ§СПЮЊ2ЭђжЛЪБЕФВнГЁжВБЛжИЪ§ЃЛвдЩЯХаЖЯжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
A.0B.1C.2D.3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() гыдВ
гыдВ![]() ЯрНЛгк
ЯрНЛгк![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌШє
ЃЌШє![]() ЃЌдђЪЕЪ§
ЃЌдђЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЪЧ__________ЃЎ
ЕФШЁжЕЗЖЮЇЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com