
(Ⅰ)现甲、乙、丙依次射击,若击中则停止射击,若击不中则下一门射击,但丙击中与否都要停止射击,求目标被击中的概率;
(Ⅱ)三门炮同时向目标射击,求击中目标的炮的门数ξ的数学期望.
科目:高中数学 来源: 题型:
| 6 |
| 5π |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012年人教B版高中数学必修3 3.4概率的应用练习卷(解析版) 题型:填空题
某中高射炮击中空中目标的概率是0.6,现在至少需要 门这样的高射炮,才能使击中空中目标的概率为99% .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
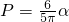 ,现有甲、乙、丙三门高射炮,每门高射炮击中目标与否相互独立,已知甲、乙、丙射击的角度分别为
,现有甲、乙、丙三门高射炮,每门高射炮击中目标与否相互独立,已知甲、乙、丙射击的角度分别为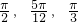 .
.查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)三门炮同时向目标射击,求恰好有两门炮击中目标的概率;
(Ⅱ)现甲、乙、丙依次射击,若击中则停止射击,若击不中则下一门射击,但丙击中与否都要停止射击,求目标被击中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com