练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数.

    （1）讨论函数的单调区间；

    （2）若函数的图象与轴相切，求证：对于任意的.

    【答案】（1）答案不唯一，具体见解析（2）证明见解析；

    【解析】

    （1）先对函数进行求导，然后根据实数的取值情况进行讨论，结合导数的正负，判断求解函数的单调性与单调区间；

    （2）因为函数的图象与轴相切，由（1）可知，且，可求出，当时，恒成立，为证明对于任意的成立，只要证明即可，令，然后在利用导数在函数最值中的应用，即可证明，由此即可证明不等式成立.

    解：（1）函数的定义域是，

    当时，，在上单调递减；

    当时，，

    在上单调递减；

    ，

    在上单调递增.

    （2）证明：因为函数的图象与轴相切，设切点为，

    ，解得，

    ，

    又当时，恒成立，

    令，

    由，得，

    是的最大值，

    ，

    成立.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】随着网上购物的普及，传统的实体店遭受到了强烈的冲击，某商场实体店近九年来的纯利润如下表所示：

    年份

    2010

    2011

    2012

    2013

    2014

    2015

    2016

    2017

    2018

    时间代号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    实体店纯利润（千万）

    2

    2.3

    2.5

    2.9

    3

    2.5

    2.1

    1.7

    1.2

    根据这9年的数据，对和作线性相关性检验，求得样本相关系数的绝对值为0.254；根据后5年的数据，对和作线性相关性检验，求得样本相关系数的绝对值为0.985；

    （1）如果要用线性回归方程预测该商场2019年实体店纯利润，现有两个方案：

    方案一：选取这9年的数据，进行预测；

    方案二：选取后5年的数据进行预测.

    从生活实际背景以及相关性检验的角度分析，你觉得哪个方案更合适.

    附：相关性检验的临界值表：

    小概率

    0.05

    0.01

    3

    0.878

    0.959

    7

    0.666

    0.798

    （2）某机构调研了大量已经开店的店主，据统计，只开网店的占调查总人数的，既开网店又开实体店的占调查总人数的，现以此调查统计结果作为概率，若从上述统计的店主中随机抽查了5位，求只开实体店的人数的分布列及期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】国家正积极推行垃圾分类工作，教育部办公厅等六部门也发布了《关于在学校推进生活垃圾分类管理工作的通知》．《通知》指出，到2020年底，各学校生活垃圾分类知识普及率要达到100%某市教育主管部门据此做了“哪些活动最能促进学生进行垃圾分类”的问卷调查（每个受访者只能在问卷的4个活动中选择一个）如图是调查结果的统计图，以下结论正确的是（ 　　）

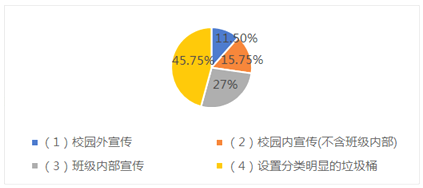
    A.回答该问卷的受访者中，选择的（2）和（3）人数总和比选择（4）的人数多

    B.回该问卷的受访者中，选择“校园外宣传”的人数不是最少的

    C.回答该问卷的受访者中，选择（4）的人数比选择（2）的人数可能多30人

    D.回答该问卷的总人数不可能是1000人

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    已知函数（是自然对数的底数）.

    （1）若曲线在处的切线也是抛物线的切线，求的值；

    （2）若对于任意恒成立，试确定实数的取值范围；

    （3）当时，是否存在，使曲线在点处的切线斜率与在上的最小值相等？若存在，求符合条件的的个数；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在传染病学中，通常把从致病刺激物侵人机体或者对机体发生作用起，到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期. 一研究团队统计了某地区1000名患者的相关信息，得到如下表格：

    潜伏期（单位：天）

    人数

    （1）求这1000名患者的潜伏期的样本平均数x (同一组中的数据用该组区间的中点值作代表) ；

    （2）该传染病的潜伏期受诸多因素的影响，为研究潜伏期与患者年龄的关系，以潜伏期是否超过6天为标准进行分层抽样，从上述1000名患者中抽取200人，得到如下列联表.请将列联表补充完整，并根据列联表判断是否有95%的把握认为潜伏期与患者年龄有关；

    潜伏期天

    潜伏期天

    总计

    岁以上（含岁）

    岁以下

    总计

    （3）以这1000名患者的潜伏期超过6天的频率，代替该地区1名患者潜伏期超过6天发生的概率，每名患者的潜伏期是否超过6天相互独立，为了深入研究，该研究团队随机调查了20名患者，其中潜伏期超过6天的人数最有可能（即概率最大）是多少？

    附：

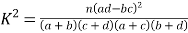    ，其中.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数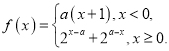给出下列四个结论：①对，，使得无解；②对，，使得有两解；③当时，，使得有解；④当时，，使得有三解.其中，所有正确结论的序号是______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （Ⅰ）若，求在区间[-1,2]上的取值范围；

    （Ⅱ）若对任意， 恒成立，记，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知抛物线的焦点为，，是抛物线上的两点，线段的垂直平分线交轴于点，若．

    （1）求点的坐标；

    （2）求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列是公差不为0的等差数列，，数列是等比数列，且，，，数列的前n项和为．

    （1）求数列的通项公式；

    （2）设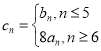，求的前n项和；

    （3）若对恒成立，求的最小值．

    查看答案和解析>>

    同步练习册答案