
如图,已知平行六面体ABCD-A1B1C1D1的底面是菱形且∠C1CB=∠C1CD=∠BCD=60°.
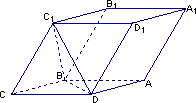
(1)证明:C1C⊥BD;
(2)假定CD=2,CC1=![]() ,记面C1BD为α,面CBD为β,求二面角α-BD-β的平面角的余弦值;
,记面C1BD为α,面CBD为β,求二面角α-BD-β的平面角的余弦值;
(3)当![]() 的值为多少时,可使A1C⊥面C1BD?
的值为多少时,可使A1C⊥面C1BD?
|
(1)证明:连结A1C1、AC,AC和BD交于点O,连结C1O, ∵四边形ABCD是菱形,∴AC⊥BD,BC=CD 又∵∠BCC1=∠DCC1,C1C是公共边,∴△C1BC≌△C1DC,∴C1B=C1D ∵DO=OB,∴C1O⊥BD,但AC⊥BD,AC∩C1O=O ∴BD⊥平面AC1,又C1C (2)解:由(1)知AC⊥BD,C1O⊥BD, ∴∠C1OC是二面角α-BD-β的平面角. 在△C1BC中,BC=2,C1C= ∴C1B2=22+( ∵∠OCB=30°,∴OB= 作C1H⊥OC,垂足为H,则H是OC中点且OH= (3)解:由(1)知BD⊥平面AC1,∵A1O |


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且| OA |
| a |
| OC |
| b |
| OO1 |
| c |
| a |
| b |
| c |
| OG |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)
如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com