
设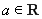 ,函数
,函数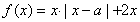 .
.
(1)若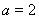 ,求函数
,求函数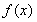 在区间
在区间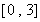 上的最大值;
上的最大值;
(2)若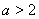 ,写出函数
,写出函数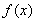 的单调区间(不必证明);
的单调区间(不必证明);
(3)若存在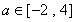 ,使得关于
,使得关于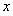 的方程
的方程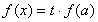 有三个不相等的实数解,求实数
有三个不相等的实数解,求实数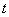 的取值范围.
的取值范围.
(1)9(2)单调递增区间是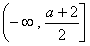 和
和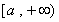 ,单调递减区间是
,单调递减区间是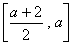 (3)
(3)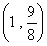
【解析】(1)当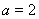 ,
,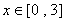 时,
时,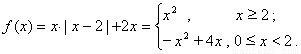

作函数图像(图像略),可知函数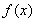 在区间
在区间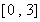 上是增函数,所以
上是增函数,所以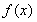 的最大值为
的最大值为 .…………(4分)
.…………(4分)
(2)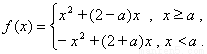 ……(1分)
……(1分)
①当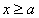 时,
时, ,
,
因为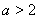 ,所以
,所以 ,
,
所以 在
在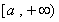 上单调递增.…………(3分)
上单调递增.…………(3分)
②当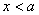 时,
时, ,
,
因为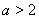 ,所以
,所以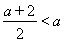 ,所以
,所以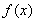 在
在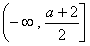 上单调递增,在
上单调递增,在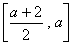 上单调递减.…………(5分)
上单调递减.…………(5分)
综上,函数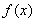 的单调递增区间是
的单调递增区间是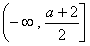 和
和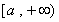 ,
,
单调递减区间是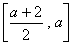 .………………(6分)
.………………(6分)
(3)①当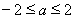 时,
时,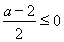 ,
,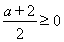 ,所以
,所以 在
在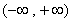 上是增函数,关于
上是增函数,关于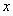 的方程
的方程 不可能有三个不相等的实数解.…………(2分)
不可能有三个不相等的实数解.…………(2分)
②当 时,由(1)知
时,由(1)知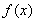 在
在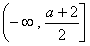 和
和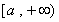 上分别是增函数,在
上分别是增函数,在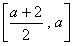 上是减函数,当且仅当
上是减函数,当且仅当 时,方程
时,方程 有三个不相等的实数解.
有三个不相等的实数解.
即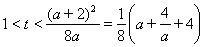 .…………(5分)
.…………(5分)
令 ,
,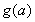 在
在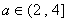 时是增函数,故
时是增函数,故 .…………(7分)
.…………(7分)
所以,实数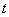 的取值范围是
的取值范围是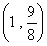 .…………(8分)
.…………(8分)


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
已知圆O1和圆O2的极坐标方程分别为ρ=2,ρ2-2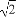 ρcos(θ-
ρcos(θ- )=2.
)=2.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程.
(2)求经过两圆交点的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
设某项试验的成功率是失败率的2倍,用随机变量X去描述1次试验的成功次数,则P(X=0)等于( )
(A)0 (B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数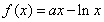 ,
,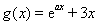 ,其中
,其中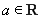 .
.
(Ⅰ)求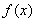 的极值;
的极值;
(Ⅱ)若存在区间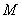 ,使
,使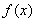 和
和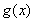 在区间
在区间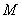 上具有相同的单调性,求
上具有相同的单调性,求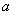 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
若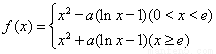 ,其中
,其中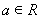 .
.
(1)当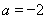 时,求函数
时,求函数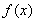 在区间
在区间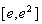 上的最大值;
上的最大值;
(2)当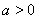 时,若
时,若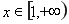 ,
,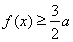 恒成立,求
恒成立,求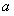 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知二次函数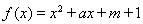 ,关于x的不等式
,关于x的不等式 的解集为
的解集为 ,其中m为非零常数.设
,其中m为非零常数.设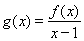 .
.
(1)求a的值;
(2)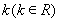 如何取值时,函数
如何取值时,函数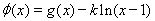 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若m=1,且x>0,求证: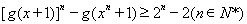
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:选择题
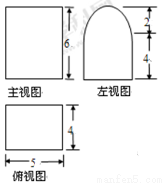
某几何体的三视图如右图(其中侧视图中的圆弧是半圆),则该几何体的表面积为( )
A.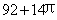 B.
B.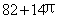 C.
C.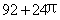 D.
D.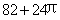
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com