
已知二次函数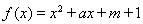 ,关于x的不等式
,关于x的不等式 的解集为
的解集为 ,其中m为非零常数.设
,其中m为非零常数.设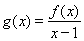 .
.
(1)求a的值;
(2)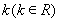 如何取值时,函数
如何取值时,函数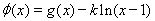 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若m=1,且x>0,求证: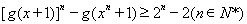
(1)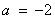 (2)当
(2)当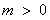 时,
时,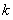 取任何实数, 函数
取任何实数, 函数 有极小值点
有极小值点 ;
;
当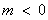 时,
时,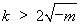 ,函数
,函数 有极小值点
有极小值点 ,有极大值点
,有极大值点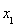 .…9分
.…9分
(其中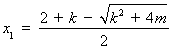 ,
, 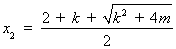 )(3)见解析
)(3)见解析
【解析】(1)【解析】
∵关于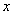 的不等式
的不等式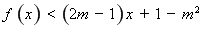 的解集为
的解集为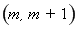 ,
,
即不等式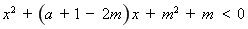 的解集为
的解集为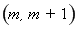 ,
,
∴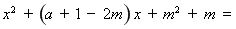
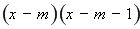 .
.
∴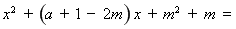
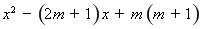 .
.
∴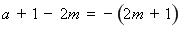 .
.
∴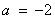 .
.
(2)解法1:由(1)得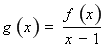
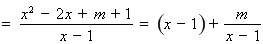 .
.
∴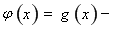
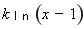
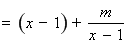
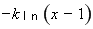 的定义域为
的定义域为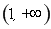 .
.
∴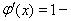
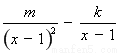
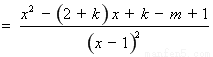 . ………3分
. ………3分
方程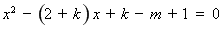 (*)的判别式
(*)的判别式
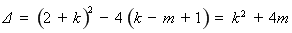 .………4分
.………4分
①当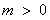 时,
时,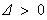 ,方程(*)的两个实根为
,方程(*)的两个实根为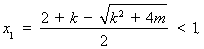
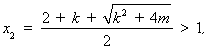 ………5分
………5分
则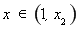 时,
时,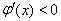 ;
;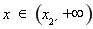 时,
时,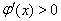 .
.
∴函数 在
在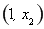 上单调递减,在
上单调递减,在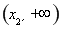 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点 . ………6分
. ………6分
②当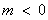 时,由
时,由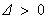 ,得
,得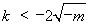 或
或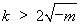 ,
,
若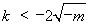 ,则
,则
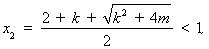
故
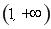 时,
时,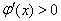 ,
,
∴函数 在
在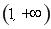 上单调递增.
上单调递增.
∴函数 没有极值点.………7分
没有极值点.………7分
若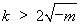 时,
时,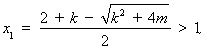
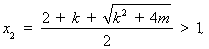
则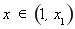 时,
时,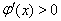 ;
;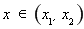 时,
时,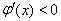 ;
;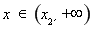 时,
时,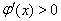 .
.
∴函数 在
在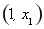 上单调递增,在
上单调递增,在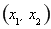 上单调递减,在
上单调递减,在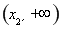 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点 ,有极大值点
,有极大值点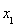 . ………8分
. ………8分
综上所述, 当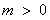 时,
时,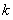 取任意实数, 函数
取任意实数, 函数 有极小值点
有极小值点 ;
;
当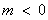 时,
时,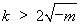 ,函数
,函数 有极小值点
有极小值点 ,有极大值点
,有极大值点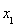 .…9分
.…9分
(其中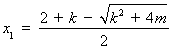 ,
, 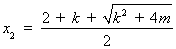 )
)
解法2:由(1)得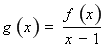
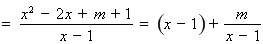 .
.
∴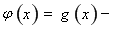
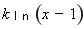
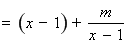
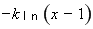 的定义域为
的定义域为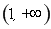 .
.
∴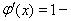
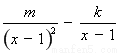
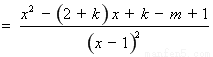 . ………3分
. ………3分
若函数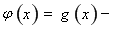
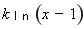 存在极值点等价于函数
存在极值点等价于函数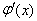 有两个不等的零点,且
有两个不等的零点,且
至少有一个零点在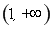 上. ………4分
上. ………4分
令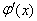
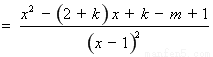
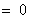 ,
,
得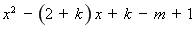
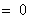 , (*)
, (*)
则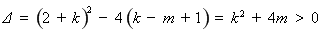 ,(**)…………5分
,(**)…………5分
方程(*)的两个实根为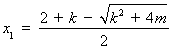 ,
, 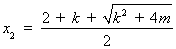 .
.
设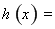
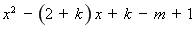 ,
,
①若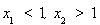 ,则
,则 ,得
,得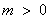 ,此时,
,此时,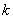 取任意实数, (**)成立.
取任意实数, (**)成立.
则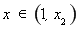 时,
时,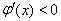 ;
;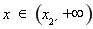 时,
时,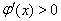 .
.
∴函数 在
在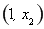 上单调递减,在
上单调递减,在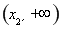 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点 . ………6分
. ………6分
②若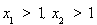 ,则
,则 得
得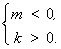
又由(**)解得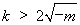 或
或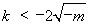 ,
,
故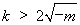 .………7分
.………7分
则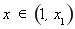 时,
时,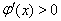 ;
;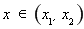 时,
时,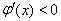 ;
;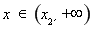 时,
时,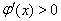 .
.
∴函数 在
在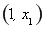 上单调递增,在
上单调递增,在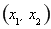 上单调递减,在
上单调递减,在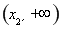 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点 ,有极大值点
,有极大值点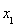 . ………8分
. ………8分
综上所述, 当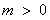 时,
时,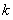 取任何实数, 函数
取任何实数, 函数 有极小值点
有极小值点 ;
;
当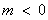 时,
时,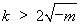 ,函数
,函数 有极小值点
有极小值点 ,有极大值点
,有极大值点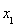 .…9分
.…9分
(其中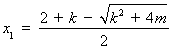 ,
, 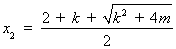 )
)
(3)∵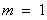 , ∴
, ∴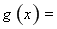
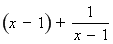 .
.
∴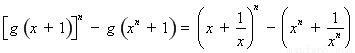
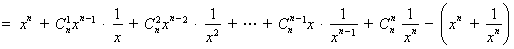
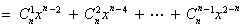 . ………10分
. ………10分
令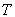
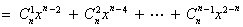 ,
,
则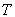

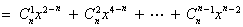 .
.
∵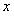
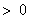 ,
,
∴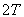
 …11分
…11分
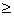
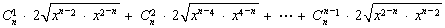 12分
12分
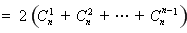

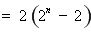 .………13分
.………13分
∴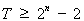 ,即
,即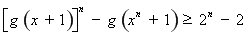 . ……………14分
. ……………14分
证法2:下面用数学归纳法证明不等式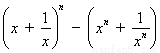
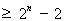 .
.
① 当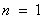 时,左边
时,左边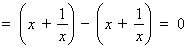 ,右边
,右边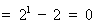 ,不等式成立;
,不等式成立;
………10分
②假设当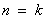
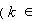 N
N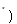 时,不等式成立,即
时,不等式成立,即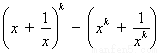
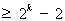 ,
,
则 
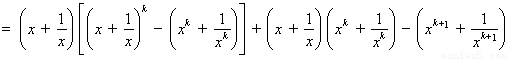
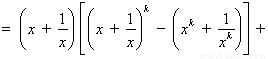
 ………11分
………11分
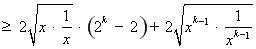 ………12分
………12分
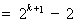 . ………13分
. ………13分
也就是说,当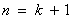 时,不等式也成立.
时,不等式也成立.
由①②可得,对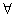
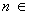 N
N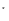 ,
,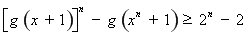 都成立. …14分
都成立. …14分


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:选择题
利用下列盈利表中的数据进行决策,应选择的方案是( )
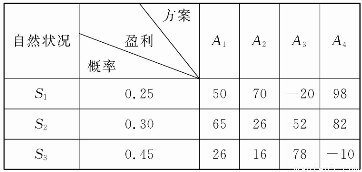
(A)A1 (B)A2 (C)A3 (D)A4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:填空题
某省实验中学高三共有学生600人,一次数学考试的成绩(试卷满分150分)服从正态分布N(100,σ2),统计结果显示学生考试成绩在80分到100分之间的人数约占总人数的 ,则此次考试成绩不低于120分的学生约有 人.
,则此次考试成绩不低于120分的学生约有 人.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
设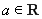 ,函数
,函数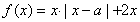 .
.
(1)若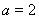 ,求函数
,求函数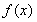 在区间
在区间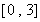 上的最大值;
上的最大值;
(2)若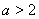 ,写出函数
,写出函数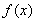 的单调区间(不必证明);
的单调区间(不必证明);
(3)若存在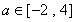 ,使得关于
,使得关于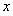 的方程
的方程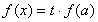 有三个不相等的实数解,求实数
有三个不相等的实数解,求实数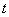 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数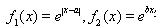
(I)若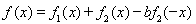 ,是否存在a,b
,是否存在a,b R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
〔II)若a=2,b=1.求函数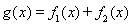 在R上的单调区间;
在R上的单调区间;
(III )对于给定的实数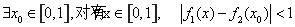 成立.求a的取值范围.
成立.求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:填空题
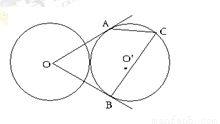
如图,两个等圆⊙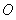 与⊙
与⊙ 外切,过
外切,过 作⊙
作⊙ 的两条切线
的两条切线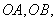
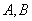 是切点,点
是切点,点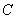 在圆
在圆 上且不与点
上且不与点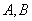 重合,则
重合,则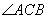 = .
= .
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:选择题
设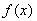 的定义域为D,若
的定义域为D,若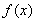 满足条件:存在
满足条件:存在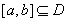 ,使
,使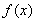 在
在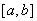 上的值域是
上的值域是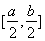 ,则称
,则称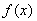 为“倍缩函数”.若函数
为“倍缩函数”.若函数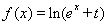 为“倍缩函数”,则t的范围是( )
为“倍缩函数”,则t的范围是( )
A . 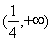 B.
B.  C.
C. 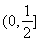 D.
D. 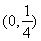
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:填空题
已知F1,F2是双曲线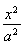 -y2=1的两个焦点,点P在此双曲线上,
-y2=1的两个焦点,点P在此双曲线上,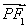 ·
·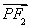 =0,如果点P到x轴的距离等于
=0,如果点P到x轴的距离等于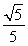 ,那么该双曲线的离心率等于________.
,那么该双曲线的离心率等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com