
【题目】如图,已知![]() 平面
平面![]() ,点
,点![]() 分别是
分别是![]() 的中点。
的中点。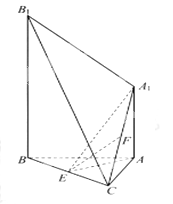
(1)求证:![]()
![]() 平面
平面![]()
(2)求证:平面![]() 平面
平面![]()
(3)求直线![]() 与平面
与平面![]() 所成角的大小
所成角的大小
【答案】
(1)
见解答
(2)
见解答
(3)
![]()
【解析】
(1)证明:如图:连接![]() 在
在![]() 中,因为
中,因为![]() 和
和![]() 分别是
分别是![]() 的中点,所以
的中点,所以![]() ,又因为
,又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
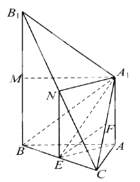
(2)因为![]() 为
为![]() 中点,所以
中点,所以![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 所以
所以![]() 平面
平面![]() ,从而
,从而![]() ,又
,又 ![]() ,所以
,所以![]() 平面
平面![]() ,又因为
,又因为 ![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() 。
。
(3)取![]() 中点
中点![]() 和
和![]() 中点
中点![]() ,连接 ,
,连接 , ![]() 因为
因为![]() 和
和![]() 分别为
分别为![]() 中点,所以
中点,所以![]() 故
故![]() 所以
所以![]() ,又因为
,又因为![]() 平面
平面 ![]() ,所以
,所以![]() 平面
平面![]() ,从而
,从而![]() 就是直线
就是直线![]() ,与平面
,与平面![]() 所成角,在
所成角,在![]() 中,可得
中,可得![]() 所以
所以![]() ,因为
,因为![]() 所以
所以![]() ,又由
,又由![]() ,有
,有![]() ,在
,在![]() 中,可得
中,可得![]() 在
在![]() 中,
中,![]() ,因此
,因此![]() ,所以,直线
,所以,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() 。
。
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则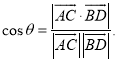 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】(2015·新课标I卷)选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线C1: x=-2,圆C2:(x-1)2+(y+2)2=1,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(1)求C1, C2的极坐标方程.
(2)若直线C3的极坐标方程为![]() ,设C2, C3的交点为M,N,求△C2MN的面积.
,设C2, C3的交点为M,N,求△C2MN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图,椭圆E:![]() (a>b>0)经过点A(0,-1),且离心率为
(a>b>0)经过点A(0,-1),且离心率为![]() .
.
(1)求椭圆E的方程;
(2)经过点(1,1),且斜率为k的直线与椭圆E交于不同两点P,Q(均异于点A),证明:直线AP与AQ的斜率之和为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() ,m 是两条不同的直线,m 垂直于平面
,m 是两条不同的直线,m 垂直于平面![]() ,则“
,则“![]() ”是“
”是“![]() " 的 ( )
" 的 ( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
据茎叶图能得到的统计结论的标号为( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分15分)某工厂某种航空产品的年固定成本为![]() 万元,每生产
万元,每生产![]() 件,需另投入成本为
件,需另投入成本为![]() ,当年产量不足
,当年产量不足![]() 件时,
件时,![]() (万元).当年产量不小于
(万元).当年产量不小于![]() 件时,
件时,![]() (万元).每件商品售价为
(万元).每件商品售价为![]() 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)年产量为多少件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖北)一种作图工具如图1所示.O是滑槽AB的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且![]() ,
,![]() .当栓子D在滑槽AB内作往复运动时,带动N绕O转动一周(D不动时,N也不动),M处的笔尖画出的曲线记为C.以O为原点,AB所在的直线为
.当栓子D在滑槽AB内作往复运动时,带动N绕O转动一周(D不动时,N也不动),M处的笔尖画出的曲线记为C.以O为原点,AB所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
(1)求曲线C的方程;
(2)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与曲线C有且只有一个公共点,试探究:
总与曲线C有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)已知椭圆E: ![]() (a>b>0)的半焦距为c,原点0到经过两点(c,0),(0,b)的直线的距离为
(a>b>0)的半焦距为c,原点0到经过两点(c,0),(0,b)的直线的距离为![]() c.
c.
(1)求椭圆E的离心率
(2)如图,AB是圆M:(x+2)2+(y-1)=![]() 的一条直径,若椭圆E经过A,B两点,求椭圆E的方程.
的一条直径,若椭圆E经过A,B两点,求椭圆E的方程.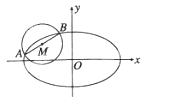
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com