练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某店销售进价为2元/件的产品，该店产品每日的销售量(单位：千件)与销售价格(单位：元/件)满足关系式，其中.

    (1)若产品销售价格为4元/件，求该店每日销售产品所获得的利润；

    (2)试确定产品的销售价格，使该店每日销售产品所获得的利润最大．(保留1位小数)

    【答案】(1)千元 ；(2) 元/件.

    【解析】

    （1）当时，销量千件，乘以每件产品的盈利，可得该店每日销售产品所获得的利润；（2）商场每日销售该产品所获得的利润等于每日销售量乘以每件产品的盈利，可得日销售量的利润函数为关于的三次多项式函数，再利用导数讨论函数的单调性，得出函数的极大值点，从而得出最大值对应的值.

    (1)当x＝4时，

    此时该店每日销售产品A所获得的利润为

    (4－2)×21＝42千元．

    (2)该店每日销售产品A所获得的利润

    ＝10＋4(x－6)2(x－2)

    ＝4x3－56x2＋240x－278(2<x<6)，

    从而f′(x)＝12x2－112x＋240

    ＝4(3x－10)(x－6)(2<x<6)．

    令f′(x)＝0，得x＝，易知在上，f′(x)>0，函数f(x)单调递增；在上，f′(x)<0，函数f(x)单调递减．

    所以x＝是函数f(x)在(2,6)内的极大值点，也是最大值点，所以当x＝≈3.3时，函数f(x)取得最大值．

    故当销售价格为3.3元/件时，利润最大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知正实数a，b，c，函数f（x）=|x+a||x+b|． （Ⅰ）若a=1，b=3，解关于x的不等式f（x）+x+1＜0；
    （Ⅱ）求证：f（1）f（c）≥16abc．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面几种推理过程是演绎推理的是 (　　)

    A. 某校高三(1)班有55人，2班有54人，3班有52人，由此得高三所有班人数超过50人

    B. 两条直线平行，同旁内角互补，如果∠A与∠B是两条平行直线的同旁内角，则∠A＋∠B＝180°

    C. 由平面三角形的性质，推测空间四边形的性质

    D. 在数列{an}中，a1＝1，an＝ (an－1＋)(n≥2)，由此归纳出{an}的通项公

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C1的参数方程为 （t为参数），以原点O为极点，以x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为 ． （I）求曲线C2的直角坐标系方程；
    （II）设M1是曲线C1上的点，M2是曲线C2上的点，求|M1M2|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)的图象与函数h(x)＝x＋＋2的图象关于点A(0,1)对称．

    (1)求函数f(x)的解析式；

    (2)若g(x)＝f(x)＋，g(x)在区间(0,2]上的值不小于6，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查50人，并将调查情况进行整理后制成如表：

    年龄（岁）

    [15，25）

    [25，35）

    [35，45）

    [45，55）

    [55，60）

    频数

    10

    10

    10

    10

    10

    赞成人数

    3

    5

    6

    7

    9


    （1）世界联合国卫生组织规定：[15，45）岁为青年，（45，60）为中年，根据以上统计数据填写以下2×2列联表：

    青年人

    中年人

    合计

    不赞成

    赞成

    合计


    （2）判断能否在犯错误的概率不超过0.05的前提下，认为赞成“车柄限行”与年龄有关？ 附： ，其中n=a+b+c+d
    独立检验临界值表：

    P（K2≥k）

    0.100

    0.050

    0.025

    0.010

    k0

    2.706

    3.841

    5.024

    6.635


    （3）若从年龄[15，25），[25，35）的被调查中各随机选取1人进行调查，设选中的两人中持不赞成“车辆限行”态度的人员为ξ，求随机变量ξ的分布列和数学期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l的参数方程为 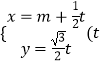为参数），以坐标原点为极点，以x轴正半轴为极轴建立极坐标系，椭圆C的极坐标方程为 ，且直线l经过椭圆C的右焦点F．
    （1）求椭圆C的内接矩形PMNQ面积的最大值；
    （2）若直线l与椭圆C交于A，B两点，求|FA||FB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，为的中点．

    求证：平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥P﹣ABCD的底面ABCD是平行四边形，△PAB与△ABC是等腰三角形，PA⊥平面ABCD，PA=2，AD=2 ，AC⊥BA，点E是线段AB上靠近点B的一个三等分点，点F、G分别在线段PD，PC上．
    （Ⅰ）证明：CD⊥AG；
    （Ⅱ）若三棱锥E﹣BCF的体积为 ，求 的值．

    查看答案和解析>>

    同步练习册答案