
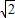 ,M为BC的中点.
,M为BC的中点.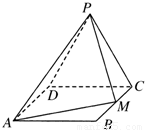
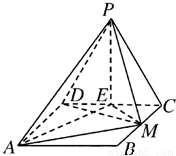
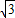 .
.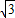 ,AM=
,AM=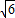 ,AE=3,
,AE=3,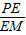 =
=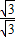 =1,∴∠PME=45°.
=1,∴∠PME=45°.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
 如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2
如图所示,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
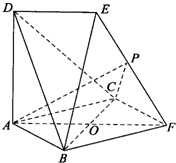 如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE=
如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年安徽皖南八校联考)(本小题满分14分)
 如图所示,边长为2的等边△
如图所示,边长为2的等边△![]() 所在的平面垂直于矩形
所在的平面垂直于矩形![]() 所在的平面,
所在的平面,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() ⊥
⊥![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示:边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直且DE=![]() ,ED//AF且∠DAF=90°。
,ED//AF且∠DAF=90°。
(1)求BD和面BEF所成的角的余弦;
|
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省高三第四次(4月)周测文科数学试卷(解析版) 题型:选择题
如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率是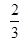 ,则阴影区域的面积为( )
,则阴影区域的面积为( )
A.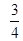 B.
B.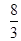 C.
C.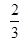 D.无法计算
D.无法计算
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com