
【题目】在平面直角坐标系![]() 中,四个点
中,四个点 ,
, ,
, ,
, 中有3个点在椭圆
中有3个点在椭圆![]() :
:![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过原点的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,设直线
两点,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,证明:存在常数
,证明:存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值.
的值.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,![]() .
.
【解析】
(1)根据椭圆的对称性可知,关于![]() 轴对称的
轴对称的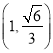 ,
, 在椭圆上.分类讨论,当
在椭圆上.分类讨论,当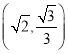 在椭圆上时,当
在椭圆上时,当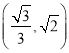 在椭圆上时,分别求解,根据
在椭圆上时,分别求解,根据![]() 确定,即可.
确定,即可.
(2)设![]() ,
,![]() ,由题意可知
,由题意可知![]() ,
,![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,与椭圆联立,变形整理得
,与椭圆联立,变形整理得![]() ,确定
,确定![]() ,
,![]() ,从而
,从而![]() ,直线
,直线![]() 的方程为
的方程为![]() ,分别令
,分别令![]() 、
、![]() 确定点
确定点![]() 与点
与点![]() 的坐标,求直线
的坐标,求直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求解即可.
,求解即可.
(1)∵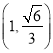 ,
, 关于
关于![]() 轴对称.
轴对称.
∴这2个点在椭圆上,即![]() ①
①
当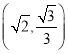 在椭圆上时,
在椭圆上时,![]() ②
②
由①②解得![]() ,
,![]() .
.
当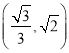 在椭圆上时,
在椭圆上时,![]() ③
③
由①③解得![]() ,
,![]() .
.
又![]()
![]()
∴![]() ,
,![]()
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,则
,则![]() .
.
因为直线![]() 的斜率
的斜率![]() ,又
,又![]() .
.
所以直线![]() 的斜率
的斜率![]() .
.
设直线![]() 的方程为
的方程为![]() ,由题意知
,由题意知![]() ,
,![]() .
.
由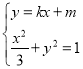 可得
可得![]() ,
,
所以![]() ,
,![]() .
.
由题意知![]() ,所以
,所以![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得
,得![]() ,即
,即![]() ,可得
,可得![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() ,可得
,可得![]() ,
,
所以![]() ,即
,即![]() ,因此,存在常数
,因此,存在常数![]() 使得结论成立.
使得结论成立.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“双曲线
”是“双曲线![]() 的离心率大于
的离心率大于![]() ”的充要条件
”的充要条件
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形”的逆否命题是假命题
是锐角三角形”的逆否命题是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着网络的普及,数码产品早已走进千家万户的生活,为了节约资源,促进资源循环利用,折旧产品回收行业得到迅猛发展,电脑使用时间越长,回收价值越低,某二手电脑交易市场对2018年回收的折旧电脑交易前使用的时间进行了统计,得到如图所示的频率分布直方图,在如图对时间使用的分组中,将使用时间落入各组的频率视为概率.
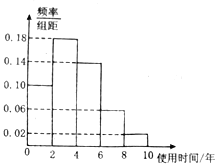
(1)若在该市场随机选取1个2018年成交的二手电脑,求其使用时间在![]() 上的概率;
上的概率;
(2)根据电脑交易市场往年的数据,得到如图所示的散点图及一些统计量的值,其中![]() (单位:年)表示折旧电脑的使用时间,
(单位:年)表示折旧电脑的使用时间,![]() (单位:百元)表示相应的折旧电脑的平均交易价格.
(单位:百元)表示相应的折旧电脑的平均交易价格.

由散点图判断,可采用![]() 作为该交易市场折旧电脑平均交易价格与使用年限
作为该交易市场折旧电脑平均交易价格与使用年限![]() 的回归方程,若
的回归方程,若![]() ,
,![]() ,选用如下参考数据,求
,选用如下参考数据,求![]() 关于
关于![]() 的回归方程,并预测在区间
的回归方程,并预测在区间![]() (用时间组的区间中点值代表该组的值)上折旧电脑的价格.
(用时间组的区间中点值代表该组的值)上折旧电脑的价格.
|
|
|
|
|
|
5.5 | 8.5 | 1.9 | 301.4 | 79.75 | 385 |
附:参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: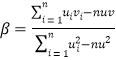 ,
,![]() .参考数据:
.参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,
,![]() 与短轴的一个端点构成一个等边三角形,且直线
与短轴的一个端点构成一个等边三角形,且直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过椭圆![]() 的左顶点
的左顶点![]() 的两条直线
的两条直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(3)在(2)的条件下求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着网络的普及,数码产品早已走进千家万户的生活,为了节约资源,促进资源循环利用,折旧产品回收行业得到迅猛发展,电脑使用时间越长,回收价值越低,某二手电脑交易市场对2018年回收的折旧电脑交易前使用的时间进行了统计,得到如图所示的频率分布直方图,在如图对时间使用的分组中,将使用时间落入各组的频率视为概率.
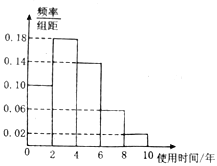
(1)若在该市场随机选取3个2018年成交的二手电脑,求至少有2个使用时间在![]() 上的概率;
上的概率;
(2)根据电脑交易市场往年的数据,得到如图所示的散点图,其中![]() (单位:年)表示折旧电脑的使用时间,
(单位:年)表示折旧电脑的使用时间,![]() (单位:百元)表示相应的折旧电脑的平均交易价格.
(单位:百元)表示相应的折旧电脑的平均交易价格.

(ⅰ)由散点图判断,可采用![]() 作为该交易市场折旧电脑平均交易价格与使用年限
作为该交易市场折旧电脑平均交易价格与使用年限![]() 的回归方程,若
的回归方程,若![]() ,
,![]() ,选用如下参考数据,求
,选用如下参考数据,求![]() 关于
关于![]() 的回归方程.
的回归方程.
|
|
|
|
|
|
5.5 | 8.5 | 1.9 | 301.4 | 79.75 | 385 |
(ⅱ)根据回归方程和相关数据,并用各时间组的区间中点值代表该组的值,估算该交易市场收购1000台折旧电脑所需的费用
附:参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: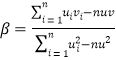 ,
,![]() .参考数据:
.参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与E交于A、B两点,且
与E交于A、B两点,且![]() ,其中O为原点.
,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为![]() ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com