
【题目】已知函数![]() ,
,![]() .
.
(![]() )设曲线
)设曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,到点
,到点![]() 的距离为
的距离为![]() ,求
,求![]() 的值.
的值.
(![]() )若对于任意实数
)若对于任意实数![]() ,
,![]() 恒成立,试确定
恒成立,试确定![]() 的取值范围.
的取值范围.
(![]() )当
)当![]() 时,是否存在实数
时,是否存在实数![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直?若存在,求出
轴垂直?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() 或
或![]() (2)
(2)![]() (3)不存在
(3)不存在
【解析】
试题
(1)该问切点横坐标已知,则利用切点在曲线上,带入曲线![]() 即可得到切点的纵坐标,对
即可得到切点的纵坐标,对![]() 进行求导并得到在切点处的导函数值即为切线的斜率,有切线的斜率,切线又过切点,利用直线的点斜式即可求的切线的方程,利用点到直线的距离公式结合条件点
进行求导并得到在切点处的导函数值即为切线的斜率,有切线的斜率,切线又过切点,利用直线的点斜式即可求的切线的方程,利用点到直线的距离公式结合条件点![]() 到切线的距离为
到切线的距离为![]() 即可求的参数
即可求的参数![]() 的值.
的值.
(2)该问为恒成立问题可以考虑分离参数法,即把参数a与x进行分离得到![]() ,则
,则![]() ,再利用函数的导函数研究函数
,再利用函数的导函数研究函数![]() 在区间
在区间![]() 的最大值,即可求的a的取值范围.
的最大值,即可求的a的取值范围.
(3)根据切线的斜率即为曲线C在切点处的导函数值,即该问可以转化为是否存在![]() 使得
使得![]() ,令
,令![]() ,则
,则![]() 即存在
即存在![]() 使得
使得![]() ,对
,对![]() 再次求导进行最值求解可得
再次求导进行最值求解可得![]() ,所以不存在
,所以不存在![]() 使得
使得![]() .
.
试题解析:
(1)![]() ,
,![]() .
.
![]() 在
在![]() 处的切线斜率为
处的切线斜率为![]() ,
,
∴切线![]() 的方程为
的方程为![]() ,即
,即![]() . 2分
. 2分
又点![]() 到切线
到切线![]() 的距离为
的距离为![]() ,所以
,所以![]() ,
,
解之得,![]() 或
或![]() 4分
4分
(2)因为![]() 恒成立,
恒成立,
若![]() 恒成立;
恒成立;
若![]() 恒成立,即
恒成立,即![]() ,在
,在![]() 上恒成立,
上恒成立,
设![]() 则
则![]()
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
所以当![]() 时,
时,![]() 取得最大值,
取得最大值,![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() . 9分
. 9分
(3)依题意,曲线![]() 的方程为
的方程为![]() ,令
,令![]()
所以![]() ,
,
设![]() ,则
,则![]() ,当
,当![]() ,
,
故![]() 在
在![]() 上单调增函数,因此
上单调增函数,因此![]() 在
在![]() 上的最小值为
上的最小值为![]()
即![]()
又![]() 时,
时,![]()
所以![]()
曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直等价于方程
轴垂直等价于方程![]() 有实数解,但是
有实数解,但是![]() ,
,![]() 没有实数解,故不存在实数
没有实数解,故不存在实数![]() 使曲线
使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直. 14分
轴垂直. 14分


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】设直线l:![]() ,圆C:
,圆C:![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.直线l与圆C有可能无公共点
B.若直线l的一个方向向量为![]() ,则
,则![]()
C.若直线l平分圆C的周长,则![]()
D.若直线l与圆C有两个不同交点M、N,则线段MN的长的最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂使用两种零件![]() 、
、![]() 装配两种产品
装配两种产品![]() 、
、![]() ,该厂的生产能力是月产
,该厂的生产能力是月产![]() 产品最多有2500件,月产
产品最多有2500件,月产![]() 产品最多有1200件;而且组装一件
产品最多有1200件;而且组装一件![]() 产品要4个
产品要4个![]() 、2个
、2个![]() ,组装一件
,组装一件![]() 产品要6个
产品要6个![]() 、8个
、8个![]() ,该厂在某个月能用的
,该厂在某个月能用的![]() 零件最多14000个;
零件最多14000个;![]() 零件最多12000个.已知
零件最多12000个.已知![]() 产品每件利润1000元,
产品每件利润1000元,![]() 产品每件2000元,欲使月利润最大,需要组装
产品每件2000元,欲使月利润最大,需要组装![]() 、
、![]() 产品各多少件?最大利润多少万元?
产品各多少件?最大利润多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出四种说法:
①设![]() 、
、![]() 、
、![]() 分别表示数据
分别表示数据![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的平均数、中位数、众数,则
的平均数、中位数、众数,则![]() ;
;
②在线性回归模型中,相关指数![]() 表示解释变量对于预报变量变化的贡献率,
表示解释变量对于预报变量变化的贡献率,![]() 越接近于
越接近于![]() ,表示回归的效果越好;
,表示回归的效果越好;
③绘制频率分布直方图时,各小长方形的面积等于相应各组的组距;
④设随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() .
.
其中不正确的是( ).
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位: ![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

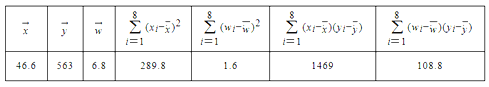
表中![]() ,
,![]() .
.
(1)根据散点图判断, ![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据(2)的结果要求:年宣传费
.根据(2)的结果要求:年宣传费![]() 为何值时,年利润最大?
为何值时,年利润最大?
附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为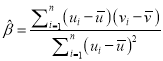 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lg(﹣x2+5x﹣6)的定义域为A,函数g(x)![]() ,x∈(0,m)的值域为B.
,x∈(0,m)的值域为B.
(1)当m=2时,求A∩B;
(2)若“x∈A”是“x∈B”的必要不充分条件,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com