
(本题满分14分)设函数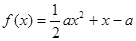 的定义域为
的定义域为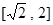 ,记函数
,记函数 的最大值为
的最大值为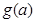 .
.
(1)求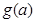 的解析式;(2)已知
的解析式;(2)已知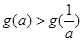 试求实数
试求实数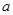 的取值范围.
的取值范围.
(1) 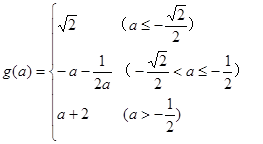 (2)
(2) 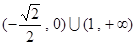
解析试题分析:(1) ( i )当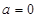 时,
时,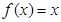 在
在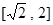 单调递增,
单调递增,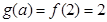 -----------1分
-----------1分
(ii)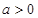 时,
时, 的对称轴为
的对称轴为 ,则
,则 在
在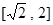 单调递增,
单调递增, 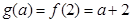 --------------2分
--------------2分
(iii)当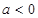 时,
时,  的对称轴为
的对称轴为 ,
,
若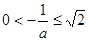 即
即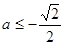 时
时 在
在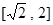 单调递减,
单调递减,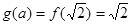 ------------------3分
------------------3分
若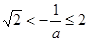 即
即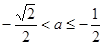 时
时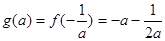 --------------------4分
--------------------4分
若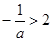 即
即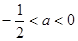 时
时 在
在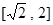 单调递增,
单调递增,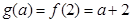 -----------------------5分
-----------------------5分
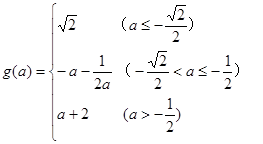 --------------------6分
--------------------6分
(2) 当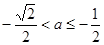 时
时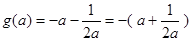 ,
,
设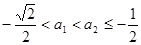 ,
,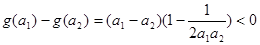 ------9分
------9分
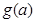 在区间
在区间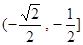 单调递增 -------------10分
单调递增 -------------10分
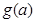 在
在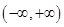 上不递减,
上不递减, 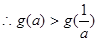 等价于
等价于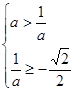 或
或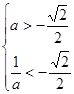 -----------12分
-----------12分
解得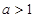 或
或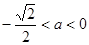 -------------------13分
-------------------13分
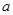 的取值范围是
的取值范围是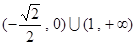 ----------14分
----------14分
考点:二次函数求最值及解不等式
点评:本题求最值时需分情况讨论,对学生来说是一个难点


科目:高中数学 来源: 题型:解答题
(本小题满分14分)
某商店如果将进价为8元的商品按每件10元售出,每天可销售200件,现在提高售价以赚取更多利润.已知每涨价0.5元,该商店的销售量会减少10件,问将售价定为多少时,才能使每天的利润最大?其最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分15分)将进货单价为80元的商品按90元一个售出时,能卖出400个,已知这种商品每个涨价1元,其销售量就减少10个,为了取得最大利润,每个售价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)广东某民营企业主要从事美国的某品牌运动鞋的加工生产,按国际惯例以美元为结算货币,依据以往加工生产的数据统计分析,若加工产品订单的金额为 万美元,可获得加工费近似为
万美元,可获得加工费近似为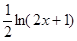 万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失
万美元,受美联储货币政策的影响,美元贬值,由于生产加工签约和成品交付要经历一段时间,收益将因美元贬值而损失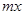 万美元,其中
万美元,其中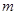 为该时段美元的贬值指数,
为该时段美元的贬值指数,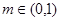 ,从而实际所得的加工费为
,从而实际所得的加工费为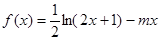 (万美元).
(万美元).
(Ⅰ)若某时期美元贬值指数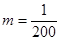 ,为确保企业实际所得加工费随
,为确保企业实际所得加工费随 的增加而增加,该企业加工产品订单的金额
的增加而增加,该企业加工产品订单的金额 应在什么范围内?
应在什么范围内?
(Ⅱ)若该企业加工产品订单的金额为 万美元时共需要的生产成本为
万美元时共需要的生产成本为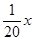 万美元,已知该企业加工生产能力为
万美元,已知该企业加工生产能力为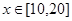 (其中
(其中 为产品订单的金额),试问美元的贬值指数
为产品订单的金额),试问美元的贬值指数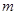 在何范围时,该企业加工生产将不会出现亏损.
在何范围时,该企业加工生产将不会出现亏损.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com