
(本小题满分10分)
定义在 上的函数
上的函数 满足
满足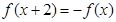 ,且当
,且当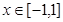 时,
时,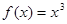 ,
,
(1)求 在
在 上的表达式;
上的表达式;
(2)若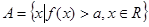 ,且
,且 ,求实数
,求实数 的取值范围。
的取值范围。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).
(Ⅰ) 求函数f(x)的表达式;
(Ⅱ) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第 个月的利润
个月的利润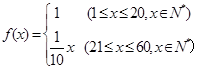 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第 个月的当月利润率
个月的当月利润率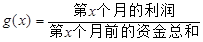 ,例如:
,例如: .
.
(Ⅰ) 求
求 ; (Ⅱ)求第
; (Ⅱ)求第 个月的当月利润率
个月的当月利润率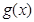 ;
;
(Ⅲ)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)已知函数
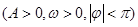 ,在同一周期内,
,在同一周期内,
当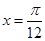 时,
时, 取得最大值
取得最大值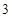 ;当
;当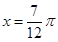 时,
时, 取得最小值
取得最小值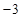 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 的单调递减区间;
的单调递减区间;
(Ⅲ)若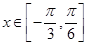 时,函数
时,函数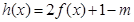 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知函数 (
( 为常数)。
为常数)。
(Ⅰ)函数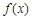 的图象在点(
的图象在点(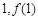 )处的切线与函数
)处的切线与函数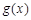 的图象相切,求实数
的图象相切,求实数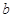 的值;
的值;
(Ⅱ)设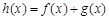 ,若函数
,若函数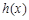 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数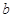 的取值范围;
的取值范围;
(Ⅲ)若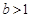 ,对于区间[1,2]内的任意两个不相等的实数
,对于区间[1,2]内的任意两个不相等的实数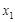 ,
,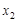 ,都有
,都有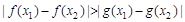 成立,求
成立,求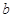 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
商店出售茶壶和茶杯,茶壶单价为每个20元,茶杯单价为每个5元,该店推出两种促销优惠办法:
(1)买1个茶壶赠送1个茶杯;
(2)按总价打9.2折付款。
某顾客需要购买茶壶4个,茶杯若干个,(不少于4个),若设购买茶杯数为x个,付款数为y(元),试分别建立两种优惠办法中y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com