练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】袋子中有四个小球，分别写有“幸”“福”“快”“乐”四个字，有放回地从中任取一个小球，取到“快”就停止，用随机模拟的方法估计直到第二次停止的概率：先由计算器产生1到4之间取整数值的随机数，且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字，以每两个随机数为一组，代表两次的结果，经随机模拟产生了20组随机数：

    13　24　12　32　43　14　24　32　31　21

    23　13　32　21　24　42　13　32　21　34

    据此估计，直到第二次就停止的概率为(　　)

    A. B.

    C. D.

    【答案】B

    【解析】由随机数表可知，在20个随机数组中，第二个数字是3的共有13 43 23 13 13共5个，所以其发生的概率为，故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

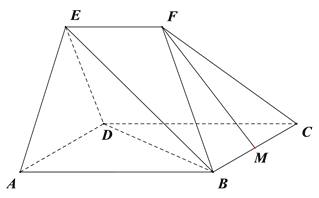
    【题目】如图，在几何体中，平面平面，四边形为菱形，且， ， ∥， 为中点．

    （Ⅰ）求证： ∥平面；

    （Ⅱ）求直线与平面所成角的正弦值；

    （Ⅲ）在棱上是否存在点，使 ？ 若存在，求的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某造船公司年造船量是20艘，已知造船x艘的产值函数为R(x)＝3 700x＋45x2－10x3(单位：万元)，成本函数为C(x)＝460x－5 000(单位：万元)．

    (1)求利润函数P(x)；(提示：利润＝产值－成本)

    (2)问年造船量安排多少艘时，可使公司造船的年利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若10y1(2)＝x02(3)，求数字x，y的值及与此两数等值的十进制数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数.

    （1）任取，记“关于的方程有一个大于1的根和一个小于1的根”为事件，求发生的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（， 为常数），函数（为自然对数的底）.

    （1）讨论函数的极值点的个数；

    （2）若不等式对恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为圆上任一点，且点．

    （1）若在圆上，求线段的长及直线的斜率．

    （2）求的最大值和最小值．

    （3）若，求的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数,．

    （1）求的单调区间;

    （2）设函数,若存在,对任意的,总有成立,求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

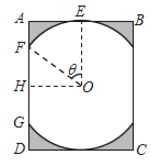
    【题目】某景区修建一栋复古建筑，其窗户设计如图所示.圆的圆心与矩形对角线的交点重合，且圆与矩形上下两边相切（为上切点），与左右两边相交（，为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域.已知圆的半径为1，且，设，透光区域的面积为.

    （1）求关于的函数关系式，并求出定义域；

    （2）根据设计要求，透光区域与矩形窗面的面积比值越大越好.当该比值最大时，求边的长度.

    查看答案和解析>>

    同步练习册答案