[题目]已知为圆上任一点.且点．(1)若在圆上.求线段的长及直线的斜率．(2)求的最大值和最小值．(3)若.求的最大值和最小值．题目和参考答案——青夏教育精英家教网—

【题目】已知为圆上任一点，且点．

（1）若在圆上，求线段的长及直线的斜率．

（2）求的最大值和最小值．

（3）若，求的最大值和最小值．

【答案】（1）；（2）

【解析】试题分析：（1）由点在圆上，可得，即得到，进而求出所以线段的长及直线的斜率；（2）由题意可得圆的圆心坐标为，半径，可得，最大值为点到圆心的距离加半径，最小值为点到圆心的距离减半径；（3）可知表示直线的斜率，设直线的斜率为，即直线的方程为，根据直线与圆的位置关系可得答案.

试题解析：（1）将代入，圆，得，所以，，．

（2）圆，圆心，，∵，∴，∴最小值为，最大值为．

（3）由题意知，即，分析可得表示该圆上的任意一点与相连所得直线的斜率，设该直线斜率为，则其方程为，又由，得，即．所以的最小值为，最大值为．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知非零向量，，，满足 =2 ﹣ ， =k + ，给出以下结论：
①若与不共线，与共线，则k=﹣2；
②若与不共线，与共线，则k=2；
③存在实数k，使得与不共线，与共线；
④不存在实数k，使得与不共线，与共线．
其中正确结论的个数是（）
A.1个
B.2个
C.3个
D.4个

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆：的短轴长为，右焦点为，点是椭圆上异于左、右顶点的一点．

（1）求椭圆的方程；

（2）若直线与直线交于点，线段的中点为，证明：点关于直线的对称点在直线上．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】袋子中有四个小球，分别写有“幸”“福”“快”“乐”四个字，有放回地从中任取一个小球，取到“快”就停止，用随机模拟的方法估计直到第二次停止的概率：先由计算器产生1到4之间取整数值的随机数，且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字，以每两个随机数为一组，代表两次的结果，经随机模拟产生了20组随机数：

13　24　12　32　43　14　24　32　31　21

23　13　32　21　24　42　13　32　21　34

据此估计，直到第二次就停止的概率为(　　)

A. B.

C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】滨湖区拟建一主题游戏园，该游戏园为四边形区域ABCD，其中三角形区城ABC为主题活动区，其中∠ACB=60°，∠ABC=45°，AB=12 m；AD、CD为游客通道（不考虑宽度），且∠ADC=120°，通道AD、CD围成三角形区域ADC为游客休闲中心，供游客休憩．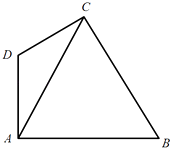

（1）求AC的长度；
（2）记游客通道AD与CD的长度和为L，求L的最大值．