练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f（x）＝log2（x＋m），且f（0）、f（2）、f（6）成等差数列．

    （1）求实数m的值；

    （2）若a、b、c是两两不相等的正数，且a、b、c成等比数列，试判断f（a）＋f(c)与2f(b)的大小关系，并证明你的结论．

     

    【答案】

    （1）m＝2．（2）f（a）＋f(c)＞2(b)．

    【解析】

    试题分析：（1）由f（0）、f（2）、f（6）成等差数列，

    可得2log2（2＋m）＝log2m＋log2（6＋m），  3分

    即（m＋2）2＝m（m＋6），且m＞0，解得m＝2．   5分

    （2）由f（x）＝log2（x＋2），

    可得2f(b)＝2log2（b＋2）＝log2（b＋2）2，    6分

    f（a）＋f(c)＝log2（a＋2）＋log2（c＋2）＝log2［（a＋2）（c＋2）］， 7分

    ∵a、b、c成等比数列，∴b2＝ac． 8分

    又a、b、c是两两不相等的正数，

    故（a＋2）（c＋2）－（b＋2）2

    ＝ac＋2（a＋c）＋4－（b2＋4b＋4）   10分

    ＝2（a＋c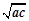－2）＝2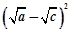＞0，    12分

    ∴log2［（a＋2）（c＋2）］＞log2（b＋2）2． 13分

    即f（a）＋f(c)＞2(b)

    考点：本题考查了数列与函数的综合运用

    点评：对于此类问题除了要求学生掌握等差（等比）数列的性质之外，还有灵活运用作差法判断大小

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)＝ax2－2x＋1，g(x)＝ln(x＋1)．

    (1)求函数y＝g(x)－x在[0,1]上的最小值；

    (2)当a≥时，函数t(x)＝f(x)＋g(x)的图像记为曲线C，曲线C在点(0,1)处的切线为l，是否存在a使l与曲线C有且仅有一个公共点？若存在，求出所有a的值；否则，说明理由．

    (3)当x≥0时，g(x)≥－f(x)＋恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年福建省福州市高三上学期期末质量检测文科数学试卷（解析版） 题型：选择题

    已知函数的图像在点A(l,f(1))处的切线l与直线x十3y＋2＝0垂直，若数列的前n项和为，则S2013的值为( )

    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2013届浙江省、兰溪一中高二下期中理科数学试卷（解析版） 题型：解答题

    （1）已知函数f(x)=x－ax+(a－1)，。讨论函数的单调性；       

    （2）.已知函数f (x)=lnx，g(x)=ex．设直线l为函数 y＝f (x) 的图象上一点A(x0，f (x0))处的切线．问在区间(1，+∞)上是否存在x0，使得直线l与曲线y=g(x)也相切．若存在，这样的x0有几个？，若没有，则说明理由。

     

    查看答案和解析>>

    科目：高中数学 来源：新课标高三数学导数专项训练（河北） 题型：解答题

    已知函数f(x)＝x3－2x2＋ax(x∈R，a∈R)，在曲线y＝f(x)的所有切线中，有且仅有一条切线l与直线y＝x垂直．

    (1)求a的值和切线l的方程；

    (2)设曲线y＝f(x)上任一点处的切线的倾斜角为θ，求θ的取值范围

     

    查看答案和解析>>

    科目：高中数学 来源：浙江省杭州十四中2011-2012学年高三2月月考试题-数学（理） 题型：解答题

     

        已知函数f （x）=lnx，g（x）=ex．

        （I）若函数φ （x） = f （x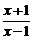）－，求函数φ （x）的单调区间；

        （Ⅱ）设直线l为函数 y＝f （x） 的图象上一点A（x0，f （x0））处的切线．证明：在区间（1，+∞）上存在唯一的x0，使得直线l与曲线y=g（x）相切．

        注：e为自然对数的底数．

     

     

     

    查看答案和解析>>

    同步练习册答案