
【题目】如图,ABCD为矩形,点A、E、B、F共面,![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() 若平面
若平面![]() ⊥平面
⊥平面![]()
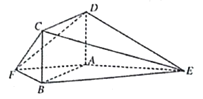
(Ⅰ)证明:平面![]() 平面ADF
平面ADF
(Ⅱ)问在线段EC上是否存在一点G,使得BG∥平面![]() 若存在,求出此时三棱锥G一ABE与三棱锥
若存在,求出此时三棱锥G一ABE与三棱锥![]() 的体积之比,若不存在,请说明理由.
的体积之比,若不存在,请说明理由.
【答案】(Ⅰ)证明见解析;(Ⅱ)存在,体积比为![]() .
.
【解析】
(1)由题意得:由ABCD为矩形可得到BC⊥AB,再由平面![]() ⊥平面
⊥平面![]() 可得到BC⊥AF,所以AF⊥平面BCF,再根据面面垂直的判断定理可得到平面
可得到BC⊥AF,所以AF⊥平面BCF,再根据面面垂直的判断定理可得到平面![]() 平面ADF;
平面ADF;
(2)通过已知条件可得到平面BCE∥平面ADF,延长EB到点H,使得BH =AF,得到ABHF是平行四边形,从而可得到HFDC是平行四边形,即有CH∥DF.,过点B作CH的平行线,交EC于点G,此点G为所求的G点即存在,由EG=![]() 和
和![]() ,可得到
,可得到![]() 即
即![]() ;
;
(Ⅰ)∵ABCD为矩形,∴BC⊥AB,
又∵平面ABCD⊥平面AEBF,BC![]() 平面ABCD,平面ABCD∩平面AEBF=AB,
平面ABCD,平面ABCD∩平面AEBF=AB,
∴BC⊥平面AEBF,
又∵AF![]() 平面AEBF,∴BC⊥AF,
平面AEBF,∴BC⊥AF,
∵∠AFB=90°,即AF⊥BF,且BC、BF![]() 平面BCF,BC∩BF=B,
平面BCF,BC∩BF=B,
∴AF⊥平面BCF,
又∵AF![]() 平面ADF,∴平面ADF
平面ADF,∴平面ADF![]() 平面BCF.
平面BCF.
(Ⅱ)∵BC∥AD,AD![]() 平面ADF,∴BC∥平面ADF.
平面ADF,∴BC∥平面ADF.
∵![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() 90°,
90°,
∴∠FAB=∠ABE=45°,∴AF∥BE,又AF![]() 平面ADF,∴BE∥平面ADF,
平面ADF,∴BE∥平面ADF,
∵BC∩BE=B,∴平面BCE∥平面ADF.
延长EB到点H,使得BH =AF,又BC ![]() AD,连CH、HF,易证ABHF是平行四边形,
AD,连CH、HF,易证ABHF是平行四边形,
∴HF![]() AB
AB![]() CD,∴HFDC是平行四边形,∴CH∥DF.
CD,∴HFDC是平行四边形,∴CH∥DF.
过点B作CH的平行线,交EC于点G,即BG∥CH∥DF,(DF![]() 平面CDF)
平面CDF)
∴BG∥平面CDF,即此点G为所求的G点,
如图:
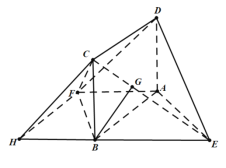
又BE=![]() ,∴EG=
,∴EG=![]() ,又
,又![]() ,
,
![]() ,
,
所以![]()


科目:高中数学 来源: 题型:
【题目】如图,四棱柱![]() ,底面
,底面![]() 为等腰梯形,
为等腰梯形,![]() ;
;![]() ,侧面
,侧面![]() 底面
底面![]() .
.
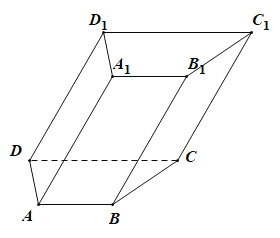
(1)在侧面![]() 中能否作一条直线使其与
中能否作一条直线使其与![]() 平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;
平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;
(2)求四面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不少于120分的有10人,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | 10 | ||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)在上述样本中从分数不少于120分的学生中,按照分层抽样的方法,抽到线上学习时间不少于5小时和线上学习时间不足5小时的学生共5名,若在这5名学生中随机抽取2人,求至少1人每周线上学习时间不足5小时的概率.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式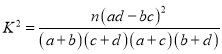 其中
其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次知识竞赛规则如下:在主办方预设的7个问题中,选手若能连续正确回答出两个问题,即停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是0.7,且每个问题的回答结果相互独立,则该选手恰好回答了5个问题就晋级下一轮的概率等于( )
A.0.07497B.0.92503C.0.1323D.0.6174
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0),F1,F2为椭圆的左右焦点,过F2的直线交椭圆与A、B两点,∠AF1B=90°,2
1(a>b>0),F1,F2为椭圆的左右焦点,过F2的直线交椭圆与A、B两点,∠AF1B=90°,2![]() ,则椭圆的离心率为( )
,则椭圆的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com