
【题目】已知函数![]() .
.
(1)讨论函数![]() 的零点个数;
的零点个数;
(2)若![]() (
(![]() 为给定的常数,且
为给定的常数,且![]() ),记
),记![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求证:
,求证:![]() .
.
【答案】(1)①当![]() 时,
时,![]() 无零点;②当
无零点;②当![]() 时,
时,![]() 有一个零点;③当
有一个零点;③当![]() 时,
时,![]() 有两个零点;(2)证明见解析.
有两个零点;(2)证明见解析.
【解析】
(1)根据解析式求得导函数,并令![]() 求得极值点.在极值点两侧,判断导函数的符号,并求得最小值.结合当
求得极值点.在极值点两侧,判断导函数的符号,并求得最小值.结合当![]() 及
及![]() 时函数值特征,即可确定零点个数.
时函数值特征,即可确定零点个数.
(2)根据![]() 及
及![]() ,可得
,可得![]() .进而确定
.进而确定![]() 的表达式,代入不等式化简变形,并令
的表达式,代入不等式化简变形,并令![]() ,构造函数
,构造函数![]() ,求得
,求得![]() 后由导函数符号判断
后由导函数符号判断![]() 的单调性及最值,即可证明不等式成立.
的单调性及最值,即可证明不等式成立.
(1)函数![]() ,
,
则![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 为单调递减;
为单调递减;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 为单调递增;
为单调递增;
所以![]() ,
,
当![]() 时
时![]() ;
;
当![]() 时
时![]() ;
;
①当![]() ,即
,即![]() 时,
时,![]() 无零点;
无零点;
②当![]() ,即
,即![]() 时,
时,![]() 有一个零点;
有一个零点;
③当![]() ,即
,即![]() 时,
时,![]() 有两个零点;
有两个零点;
(2)证明:因为![]() ,
,
所以![]() ,
,
由(1)可知![]() 在区间
在区间![]() 上的最小值
上的最小值![]() ,
,
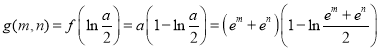 ,
,
所以不等式![]() 可化为
可化为
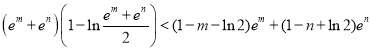 ,
,
移项化简可得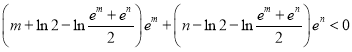 ,
,
所以![]() ,
,
即![]() ,
,
令![]() ,则
,则![]() .
.
所以原不等式可化为![]() ,
,
令![]() .
.
则![]() ,
,
所以![]() 在
在![]() 单调递减,
单调递减,
则![]() ,
,
即![]() 成立,
成立,
原不等式得证.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】如图,ABCD为矩形,点A、E、B、F共面,![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() 若平面
若平面![]() ⊥平面
⊥平面![]()
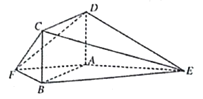
(Ⅰ)证明:平面![]() 平面ADF
平面ADF
(Ⅱ)问在线段EC上是否存在一点G,使得BG∥平面![]() 若存在,求出此时三棱锥G一ABE与三棱锥
若存在,求出此时三棱锥G一ABE与三棱锥![]() 的体积之比,若不存在,请说明理由.
的体积之比,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,__________,求△
,__________,求△![]() 的周长
的周长![]() 和面积
和面积![]() .
.
在①![]() ,
,![]() ,②
,②![]() ,
,![]() ,③
,③![]() ,
,![]() 这三个条件中,任选一个补充在上面问题中的横线处,并加以解答.
这三个条件中,任选一个补充在上面问题中的横线处,并加以解答.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(I)判断曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 的公共点个数;
的公共点个数;
(II)若函数![]() 有且仅有一个零点,求
有且仅有一个零点,求![]() 的值;
的值;
(III)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的两个顶点坐标是
的两个顶点坐标是![]() ,
,![]() ,
,![]() 的周长为
的周长为![]() ,
,![]() 是坐标原点,点
是坐标原点,点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若互相平行的两条直线![]() ,
,![]() 分别过定点
分别过定点![]() 和
和![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若四边形
两点,若四边形![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线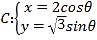 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程
的极坐标方程![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
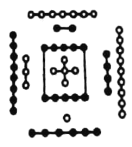
【题目】《易·系辞上》有“河出图,洛出书”之说.河图、洛书是中国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”,是中华文化,阴阳术数之源.其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中,如图,白圈为阳数,黑点为阴数,若从阴数和阳数中各取一数,则其差的绝对值为1的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com