
【题目】如图,已知圆柱内有一个三棱锥![]() ,
,![]() 为圆柱的一条母线,
为圆柱的一条母线,![]() ,
,![]() 为下底面圆
为下底面圆![]() 的直径,
的直径,![]() ,
,![]() .
.
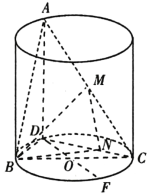
(1)在圆柱的上底面圆内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
(2)设点![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)当点![]() 为上底面圆的圆心时,证明见解析.(2)
为上底面圆的圆心时,证明见解析.(2)![]()
【解析】
(1)当点![]() 为上底面圆的圆心时,
为上底面圆的圆心时,![]() 平面
平面![]() ,取上底面圆的圆心为
,取上底面圆的圆心为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,先证明四边形
,先证明四边形![]() 为平行四边形,可得到
为平行四边形,可得到![]() ,然后可得四边形
,然后可得四边形![]() 为平行四边形,然后得到
为平行四边形,然后得到![]() 即可.
即可.
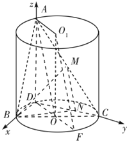
(2)以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,算出平面
,算出平面![]() 的法向量,平面
的法向量,平面![]() 的一个法向量为
的一个法向量为![]() ,然后算出答案即可.
,然后算出答案即可.
(1)当点![]() 为上底面圆的圆心时,
为上底面圆的圆心时,![]() 平面
平面![]() .
.
证明如下:
如图,取上底面圆的圆心为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,所以
,所以![]() .
.
又![]() ,所以四边形
,所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
故点![]() 为上底面圆的圆心
为上底面圆的圆心![]() 时,
时,![]() 平面
平面![]() .
.
(2)以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() .
.
于是可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由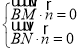 ,得
,得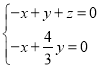 .
.
令![]() ,则可取
,则可取![]() .
.
取平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,则
,则
![]() ,
,
故平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
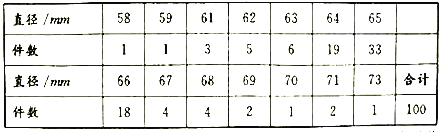
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(I)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行判定(
,并根据以下不等式进行判定(![]() 表示相应事件的概率):
表示相应事件的概率):
①![]() ;
;
②![]() ;
;
③![]() .
.
判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙,若仅满足其中一个,则等级为丙;若全部都不满足,则等级为了.试判断设备![]() 的性能等级.
的性能等级.
(Ⅱ)将直径尺寸在![]() 之外的零件认定为是“次品”.
之外的零件认定为是“次品”.
①从设备![]() 的生产流水线上随机抽取2个零件,求其中次品个数
的生产流水线上随机抽取2个零件,求其中次品个数![]() 的数学期望
的数学期望![]() ;
;
②从样本中随意抽取2个零件,求其中次品个数![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为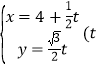 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建建立极坐标系,曲线C的极坐标方程为![]() .
.
![]() 求曲线C的直角坐标方程与直线l的极坐标方程;
求曲线C的直角坐标方程与直线l的极坐标方程;
![]() Ⅱ
Ⅱ![]() 若直线
若直线![]() 与曲线C交于点
与曲线C交于点![]() 不同于原点
不同于原点![]() ,与直线l交于点B,求
,与直线l交于点B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,其岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.某市2019年这几类工作岗位的薪资(单位:万元/月)情况如下表所示:
薪资
岗位 |
|
|
|
|
数据开发 |
|
|
|
|
数据分析 |
|
|
|
|
数据挖掘 |
|
|
|
|
数据产品 |
|
|
|
|
由表中数据可得该市各类岗位的薪资水平高低情况为( )
A.数据挖掘>数据开发>数据产品>数据分析
B.数据挖掘>数据产品>数据开发>数据分析
C.数据挖掘>数据开发>数据分析>数据产品
D.数据挖掘>数据产品>数据分析>数据开发
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆柱内有一个三棱锥![]() ,
,![]() 为圆柱的一条母线,
为圆柱的一条母线,![]() ,
,![]() 为下底面圆
为下底面圆![]() 的直径,
的直径,![]() ,
,![]() .
.

(1)在圆柱的上底面圆内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
(2)设点![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组为了研究一种治疗新冠肺炎患者的新药的效果,选50名患者服药一段时间后,记录了这些患者的生理指标![]() 和
和![]() 的数据,并统计得到如下的
的数据,并统计得到如下的![]() 列联表(不完整):
列联表(不完整):
|
| 合计 | |
| 12 | 36 | |
| 7 | ||
合计 |
其中在生理指标![]() 的人中,设
的人中,设![]() 组为生理指标
组为生理指标![]() 的人,
的人,![]() 组为生理指标
组为生理指标![]() 的人,他们服用这种药物后的康复时间(单位:天)记录如下:
的人,他们服用这种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,25
组:12,13,15,16,17,14,25
(Ⅰ)填写上表,并判断是否有95%的把握认为患者的两项生理指标![]() 和
和![]() 有关系;
有关系;
(Ⅱ)从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
附: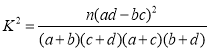 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,AB是圆O:x2+y2=1的直径,且点A在第一象限;圆O1:(x﹣a)2+y2=r2(a>0)与圆O外离,线段AO1与圆O1交于点M,线段BM与圆O交于点N,且![]() ,则a的取值范围为_______.
,则a的取值范围为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】桥牌是一种高雅、文明、竞技性很强的智力性游戏.近年来,在中国桥牌协会“桥牌进校园”活动的号召下,全国各地中小学纷纷积极加入到青少年桥牌推广的大营中.为了了解学生对桥牌这项运动的兴趣,某校从高一学生中随机抽取了200名学生进行调查,经统计男生与女生的人数之比为2:3,男生中有50人对桥牌有兴趣,女生中有20人对桥牌不感兴趣.
(1)完成2×2列联表,并回答能否有![]() 的把握认为“该校高一学生对桥牌是否感兴趣与性别有关”?
的把握认为“该校高一学生对桥牌是否感兴趣与性别有关”?
感兴趣 | 不感兴趣 | 合计 | |
男 | 50 | —— | —— |
女 | —— | 20 | —— |
合计 | —— | —— | 200 |
(2)从被调查的对桥牌有兴趣的学生中利用分层抽样抽取6名学生,再从6名学生中抽取2名学生作为桥牌搭档参加双人赛.求抽到一名男生与一名女生的概率.
附:参考公式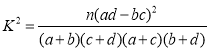 ,其中
,其中![]() .
.
临界值表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com