
(本题满分12分)
已知函数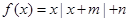 ,其中
,其中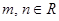
(1)
若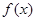 为R上的奇函数,求
为R上的奇函数,求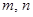 的值;
的值;
(2)
若常数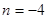 ,且
,且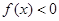 对任意
对任意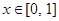 恒成立,求
恒成立,求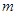 的取值范围.
的取值范围.
(Ⅰ)
 (Ⅱ)
(Ⅱ) .
.
【解析】本试题主要是考查了函数的奇偶性以及函数与不等式的关系的运用。
(1)若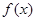 为奇函数,
为奇函数,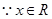 ,
, ,即
,即

 由
由 ,有
,有 ,
,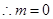 -
-
(2)常数 ,且
,且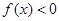 对任意
对任意 恒成立,则只需要研究函数的最大值小于零即可,得到参数m的范围。
恒成立,则只需要研究函数的最大值小于零即可,得到参数m的范围。
解:(Ⅰ)
若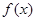 为奇函数,
为奇函数,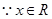 ,
, ,即
,即
 ,---2分
,---2分
 由
由 ,有
,有 ,
,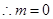 ---4分
---4分
此时,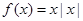 是R上的奇函数,故所求
是R上的奇函数,故所求 的值为
的值为
(Ⅱ) ① 当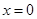 时,
时,  恒成立,
恒成立, ----6分
----6分
② 当 时,原不等式可变形为
时,原不等式可变形为 即
即 恒成立—7分
恒成立—7分
∴ 只需对 ,满足
,满足
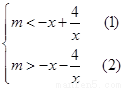 恒成立-----9分
恒成立-----9分
对(1)式:令 ,当
,当 时,
时, ,
,
则 在
在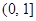 上单调递减,
上单调递减,
对(2)式:令 ,当
,当 时,
时, ,
,
则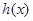 在
在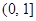 上单调递增,
上单调递增, ---11分
---11分
由①、②可知,所求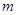 的取值范围是
的取值范围是
 .---12分
.---12分


科目:高中数学 来源: 题型:
| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海市金山区高三上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分12分,第1小题6分,第2小题6分)
已知集合A={x| | x–a | < 2,xÎR
},B={x| <1,xÎR }.
<1,xÎR }.
(1) 求A、B;
(2) 若 ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省高三10月月考理科数学试卷(解析版) 题型:解答题
(本题满分12分)
设函数 (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
.
(1)求 的解析式;
的解析式;
(2)证明:曲线 的图像是一个中心对称图形,并求其对称中心.
的图像是一个中心对称图形,并求其对称中心.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三第二次月考文科数学 题型:解答题
(本题满分12分,(Ⅰ)小问4分,(Ⅱ)小问6分,(Ⅲ)小问2分.)
如图所示,直二面角 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
(Ⅰ)求证: ⊥平面
⊥平面
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com