
【题目】定义在![]() 上的函数
上的函数![]() ,给出下列四个命题:
,给出下列四个命题:
①若![]() 是偶函数,则
是偶函数,则![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
②若![]() ,则
,则![]() 的图像关于点
的图像关于点![]() 对称;
对称;
③若![]() ,且
,且![]() ,则
,则![]() 的一个周期为2;
的一个周期为2;
④![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
其中正确命题的序号为________
【答案】②③
【解析】
①若f(x)是偶函数,则f(x)的图象关于y轴对称,f(x+1)的图象可由f(x)图象向左平移1个单位得到,即可判断;
②由f(x+a)+f(a﹣x)=2b,则f(x)的图象关于点(a,b)对称,即可判断;
③由函数的对称性得f(x+6)=f(﹣x),且f(x+8)=f(﹣x),即有f(x+2)=f(x),即可判断;
④令x+3=t,则x=t﹣3,则y=f(t)和y=f(6﹣t)的图象关于t=3对称,即可判断.
①若f(x)是偶函数,则f(x)的图象关于y轴对称,
f(x+1)的图象可由f(x)图象向左平移1个单位得到,
故图象关于直线x=﹣1对称,故①错;
②若f(x+3)=﹣f(3﹣x),即f(3+x)+f(3﹣x)=0,
则f(x)的图象关于点(3,0)对称,故②对;
③若f(x+3)=f(3﹣x),且f(x+4)=f(4﹣x),
则f(x+6)=f(﹣x),且f(x+8)=f(﹣x),即有f(x+6)=f(x+8)即有f(x+2)=f(x),
则f(x)的一个周期为2,故③对;
④令x+3=t,则x=t﹣3,则y=f(t)和y=f(6﹣t)的图象关于t=3对称,
则y=f(x+3)与y=f(3﹣x)的图象关于直线x=0对称,故④错.
故答案为:②③.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】(本题满分12分) 如图,![]() 的外接圆
的外接圆![]() 的半径为
的半径为![]() ,
,![]() 所在的平面,
所在的平面,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
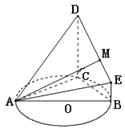
(1)求证:平面ADC![]() 平面BCDE.
平面BCDE.
(2)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为![]() ?若存在,
?若存在,
确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A. 命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B. 若![]() 为假命题,则
为假命题,则![]() 均为假命题
均为假命题
C. 对于命题![]() :
:![]()
![]() ,使得
,使得![]() ,则
,则![]() :
:![]()
![]() ,均有
,均有![]()
D. “![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000t生活垃圾.经分拣以后数据统计如下表(单位:![]() ):根据样本估计本市生活垃圾投放情况,下列说法错误的是( )
):根据样本估计本市生活垃圾投放情况,下列说法错误的是( )
厨余垃圾”箱 | 可回收物”箱 | 其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
A.厨余垃圾投放正确的概率为![]()
B.居民生活垃圾投放错误的概率为![]()
C.该市三类垃圾箱中投放正确的概率最高的是“可回收物”箱
D.厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量的方差为20000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() 上的动点
上的动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等.
的距离相等.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 分别作射线
分别作射线![]() 、
、![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,且
,且![]() .试探究直线
.试探究直线![]() 是否过定点?如果是,请求出该定点;如果不是,请说明理由
是否过定点?如果是,请求出该定点;如果不是,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 且
且![]() .
.
(1)求实数![]() 的值;
的值;
(2)判断函数![]() 在区间
在区间![]() 上的单调性,并用函数单调性的定义证明;
上的单调性,并用函数单调性的定义证明;
(3)求实数![]() 的取值范围,使得关于
的取值范围,使得关于![]() 的方程
的方程![]() 分别为:
分别为:
①有且仅有一个实数解;②有两个不同的实数解;③有三个不同的实数解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】临近2020年春节,西宁市各卖场挖空心思寻找促销策略.商人张三丰善于运用数学思维进行销售分析,他根据以往当地的需求情况,得出如下他所经营的某种产品日需求量的频率分布直方图.
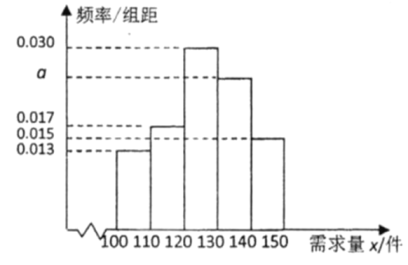
(1)求图中![]() 的值,并估计日需求量的众数:
的值,并估计日需求量的众数:
(2)某日,张三丰购进130件该种产品,根据近期市场行情,当天每售出1件能获利30元,未售出的部分,每件亏损20元设当天的需求量为![]() 件
件![]() ,纯利润为
,纯利润为![]() 元
元
(i)将![]() 表示为
表示为![]() 的函数;(ii)根据直方图估计当天纯利润
的函数;(ii)根据直方图估计当天纯利润![]() 不少于3400元的概率.
不少于3400元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com