
【题目】已知椭圆C: ![]() 的长轴长为4,焦距为
的长轴长为4,焦距为![]() .
.
(Ⅰ)求椭圆C的方程;

(Ⅱ)过动点M(0,m)(m>0)的直线交x轴与点N,交C于点A,P(P在第一象限),且M是线段PN的中点,过点P作x轴的垂线交C于另一点Q,延长线QM交C于点B.
(i)设直线PM、QM的斜率分别为k、![]() ,证明
,证明![]() 为定值.
为定值.
(ii)求直线AB的斜率的最小值.
【答案】(Ⅰ) ![]() ;(Ⅱ)(i)证明见解析;(ii)
;(Ⅱ)(i)证明见解析;(ii) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意可得![]() ,椭圆C的方程为
,椭圆C的方程为![]() .
.
(Ⅱ)(i)设![]() ,由题意可得
,由题意可得![]() ,结合斜率公式可得PM的斜率
,结合斜率公式可得PM的斜率![]() ,QM的斜率
,QM的斜率![]() ,故
,故![]() 为定值-3.
为定值-3.
(ii)设![]() ,直线PA的方程为
,直线PA的方程为![]() ,与椭圆方程联立可得
,与椭圆方程联立可得![]() .则
.则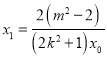 ,
,  ,同理
,同理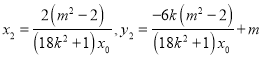 ,故
,故![]() .结合均值不等式的结论可得当且仅当
.结合均值不等式的结论可得当且仅当![]() 时,直线AB的斜率有最小值为
时,直线AB的斜率有最小值为![]() .
.
试题解析:
(Ⅰ)设椭圆的半焦距为c,
由题意知![]() ,
,
所以![]() ,
,
所以椭圆C的方程为![]() .
.
(Ⅱ)(i)设![]() ,
,
由![]() ,可得
,可得![]() ,
,
所以直线PM的斜率![]() ,
,
直线QM的斜率![]() ,
,
此时![]() ,所以
,所以![]() 为定值-3.
为定值-3.
(ii)设![]() ,
,
直线PA的方程为![]() ,
,
直线QB的方程为![]() ,
,
联立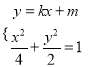 ,
,
整理得![]() .
.
由![]() 可得
可得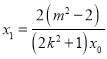 ,
,
所以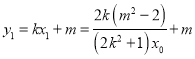 ,
,
同理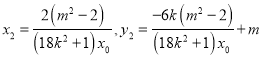 ,
,
所以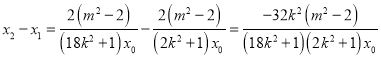 ,
,
 ,
,
所以![]() .
.
由![]() ,可知
,可知![]() ,
,
所以![]() ,等号当且仅当
,等号当且仅当![]() 时取得,
时取得,
此时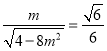 ,即
,即![]() ,符合题意,
,符合题意,
所以直线AB的斜率的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】片森林原来面积为a,计划每年砍伐森林面积是上一年末森林面积的p%,当砍伐到原来面积的一半时,所用时间是10年,已知到今年末为止,森林剩余面积为原来面积的![]() ,为保护生态环境,森林面积至少要保留原来面积的
,为保护生态环境,森林面积至少要保留原来面积的![]() .
.
(1)求每年砍伐面积的百分比p%;
(2)到今年为止,该森林已砍伐了多少年?
(3)今年以后至多还能再砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且![]() .将角α的终边按逆时针方向旋转
.将角α的终边按逆时针方向旋转![]() ,交单位圆于点B.记A(x1,y1),B(x2,y2).
,交单位圆于点B.记A(x1,y1),B(x2,y2).
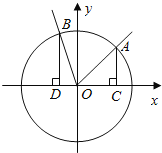
(Ⅰ)若![]() ,求x2;
,求x2;
(Ⅱ)分别过A,B作x轴的垂线,垂足依次为C,D.记△AOC的面积为S1,△BOD的面积为S2.若S1=2S2,求角α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.

(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求证:AC∥平面DEF;
(Ⅲ)求三棱锥A—DEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把下列演绎推理写成三段论的形式.
(1)在标准大气压下,水的沸点是100℃,所以在标准大气压下把水加热到100℃时,水会沸腾;
(2)一切奇数都不能被2整除, ![]() 是奇数,所以
是奇数,所以![]() 不能被2整除;
不能被2整除;
(3)三角函数都是周期函数, ![]() 是三角函数,因此
是三角函数,因此![]() 是周期函数.
是周期函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() (直接写出结果即可);
(直接写出结果即可);
(2)根据表格中的数据作出![]() 一个周期的图象;
一个周期的图象;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com