
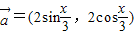 ,
,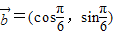 ,函数
,函数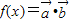 (x∈R).
(x∈R).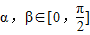 ,
,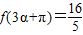 ,
,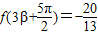 ,求cos(α+β)的值.
,求cos(α+β)的值.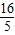 可求得cosα与sinα的值;同理,由f(3β+
可求得cosα与sinα的值;同理,由f(3β+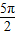 )=-
)=-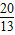 ,可求得sinβ与cosβ的值,从而可求cos(α+β).
,可求得sinβ与cosβ的值,从而可求cos(α+β).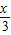 cos
cos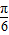 +2cos
+2cos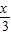 sin
sin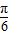 =2sin(
=2sin(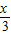 +
+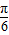 )(4分)
)(4分)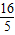 得4sin[
得4sin[ (3α+π)+
(3α+π)+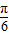 ]=
]=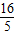 ,
,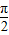 )=
)=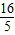 ,
, ,
,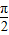 ],
],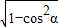 =
= ,(8分)
,(8分)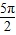 )=-
)=-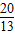 ,
, (3β+
(3β+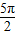 )+
)+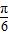 ]=-
]=-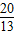 ,即4sin(β+π)=-
,即4sin(β+π)=-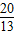 ,
,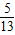 ,又∵β∈[0,
,又∵β∈[0,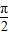 ],
],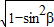 =
=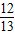 ,(12分)
,(12分) ×
×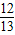 -
- ×
×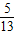 =
=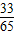 (14分)
(14分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014届浙江省高一下学期期末考试文科数学试卷(解析版) 题型:解答题
已知向量 ,设函数
,设函数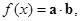 其中xÎR.
其中xÎR.
(1)求函数 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
(2)将函数 的图象的纵坐标保持不变,横坐标扩大到原来的两倍,然后再向右平移
的图象的纵坐标保持不变,横坐标扩大到原来的两倍,然后再向右平移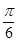 个单位得到
个单位得到 的图象,求
的图象,求 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源:0103 模拟题 题型:解答题
 ,
,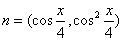 ,函数f(x)=m·n。
,函数f(x)=m·n。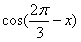 的值;
的值;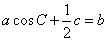 ,求f(2B)的取值范围。
,求f(2B)的取值范围。 查看答案和解析>>
科目:高中数学 来源:天津模拟题 题型:解答题
 ,设函数f(x)=m·n-1,
,设函数f(x)=m·n-1,  ,求
,求 的值.
的值. 查看答案和解析>>
科目:高中数学 来源:2010年浙江省温州市摇篮杯高一数学竞赛试卷(解析版) 题型:解答题
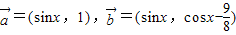 ,设函数
,设函数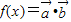 ,x∈[0,π]
,x∈[0,π]查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com