
【题目】已知椭圆![]() ,经过点
,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .
.
(1)若![]() ,且
,且![]() 恰为线段
恰为线段![]() 的中点,求证:线段
的中点,求证:线段![]() 的垂直平分线经过定点;
的垂直平分线经过定点;
(2)若![]() ,设
,设![]() 分别为
分别为![]() 的左、右顶点,直线
的左、右顶点,直线![]() 、
、![]() 相交于点
相交于点![]() .当点
.当点![]() 异于
异于![]() 时,
时,![]() 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.
【答案】(1)证明见解析;(2)是,4.
【解析】
(1)设![]() ,
,![]() ,由
,由![]() 是椭圆
是椭圆![]() 上的点可得
上的点可得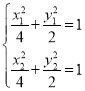 ,两式相减进行整理可得
,两式相减进行整理可得![]() ,从而可求出
,从而可求出![]() ,则可得
,则可得![]() 的垂直平分线的斜率,由点斜式可得
的垂直平分线的斜率,由点斜式可得![]() 的垂直平分线的方程为
的垂直平分线的方程为![]() ,即可得所过定点.
,即可得所过定点.
(2)由点斜式得直线![]() 的方程为
的方程为![]() ,则点
,则点![]() 从而可求
从而可求![]() ;
;
得直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立可求出其交点横坐标
,联立可求出其交点横坐标![]() ,联立
,联立![]() 与椭圆方程,结合韦达定理,对
与椭圆方程,结合韦达定理,对![]() 进行化简,可得
进行化简,可得![]()
![]() ,即可求出
,即可求出![]() 的值,从而可判断是否为定值.
的值,从而可判断是否为定值.
解:设![]() ,
,![]() .
.
(1)由题意知,直线![]() 的斜率为
的斜率为![]() ,因为
,因为![]() 是椭圆
是椭圆![]() 上的点,则
上的点,则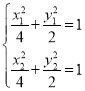 ,
,
两式相减,整理得![]() ,所以
,所以![]() ,故线段
,故线段![]() 的垂直平分线的斜率为
的垂直平分线的斜率为![]() ,
,
从而线段![]() 的垂直平分线的方程为
的垂直平分线的方程为![]() ,
,
所以,线段![]() 的垂直平分线经过定点
的垂直平分线经过定点![]() .
.
(2)直线![]() 的方程为
的方程为![]() ,由条件知:
,由条件知:![]() ,则点
,则点![]() ,
,![]() .
.
联立直线![]() 与椭圆
与椭圆![]() 的方程,消去
的方程,消去![]() 得:
得:![]() ,
,
所以![]() ,
,![]() .
.
直线![]() 的方程为
的方程为![]() ①,直线
①,直线![]() 的方程为
的方程为![]() ②.
②.
设点![]() ,由①,②得,
,由①,②得,![]()
![]()
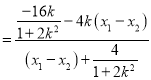
![]() .
.
所以,![]() .即
.即![]() 为定值4.
为定值4.


科目:高中数学 来源: 题型:
【题目】某校开展学生社会法治服务项目,共设置了文明交通,社区服务,环保宣传和中国传统文化宣讲四个项目,现有该校的甲、乙、丙、丁4名学生,每名学生必须且只能选择1项.
(1)求恰有2个项目没有被这4名学生选择的概率;
(2)求“环保宣传”被这4名学生选择的人数![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020元旦联欢晚会上,![]() ,
,![]() 两班各设计了一个摸球表演节目的游戏:
两班各设计了一个摸球表演节目的游戏:![]() 班在一个纸盒中装有1个红球,1个黄球,1个白球,这些球除颜色外完全相同,记事件
班在一个纸盒中装有1个红球,1个黄球,1个白球,这些球除颜色外完全相同,记事件![]() :同学们有放回地每次摸出1个球,重复
:同学们有放回地每次摸出1个球,重复![]() 次,
次,![]() 次摸球中既有红球,也有黄球,还有白球;
次摸球中既有红球,也有黄球,还有白球;![]() 班在一个纸盒中装有1个蓝球,1个黑球,这些球除颜色外完全相同,记事件
班在一个纸盒中装有1个蓝球,1个黑球,这些球除颜色外完全相同,记事件![]() :同学们有放回地每次摸出1个球,重复
:同学们有放回地每次摸出1个球,重复![]() 次,
次,![]() 次摸球中既有蓝球,也有黑球,事件
次摸球中既有蓝球,也有黑球,事件![]() 发生的概率为
发生的概率为![]() ,事件
,事件![]() 发生的概率为
发生的概率为![]() .
.
(1)求概率![]() ,
,![]() 及
及![]() ,
,![]() ;
;
(2)已知![]() ,其中
,其中![]() ,
,![]() 为常数,求
为常数,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为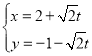 (t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,且直线l与曲线C交于M、N两点.
,且直线l与曲线C交于M、N两点.
(1)求直线l的普通方程以及曲线C的直角坐标方程;
(2)若曲线C外一点![]() 恰好落在直线l上,且
恰好落在直线l上,且![]() ,求m,n的值.
,求m,n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是以
是以![]() 为直径的圆上一点,
为直径的圆上一点,![]() ,等腰梯形
,等腰梯形![]() 所在的平面垂直于⊙
所在的平面垂直于⊙![]() 所在的平面,且
所在的平面,且![]() .
.
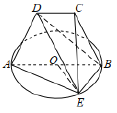
(1)求![]() 与
与![]() 所成的角;
所成的角;
(2)若异面直线![]() 和
和![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
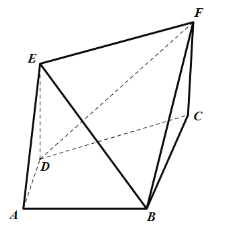
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点P,使得直线
上是否存在点P,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,
中,
曲线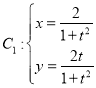 (
(![]() 为参数),
为参数),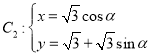 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() (
(![]() 且
且![]() ).
).
(1)求![]() 与
与![]() 的极坐标方程;
的极坐标方程;
(2)若![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,当
,当![]() 为何值时,
为何值时,![]() 最大,并求最大值.
最大,并求最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com