【题目】已知有一个三边长分别为3,4,5的三角形.求下面两只蚂蚁与三角形三顶点的距离均超过1的概率.(1)一只蚂蚁在三角形的边上爬行(2)一只蚂蚁在三角形所在区域内部爬行
【答案】（1）
.
（2）
.
【解析】
（1）根据题意，做出三角形的图形，可设为
，易得可得其周长，再在其三边上找到距离定点距离为1的6个点，即
，进而图分析可得，距离三角形的三个顶点的距离均超过1的部分为线段
上，易得其长度，由几何概型公式计算可得答案．
记“蚂蚁与三角形三顶点的距离均超过1”为事件A.
(1) 
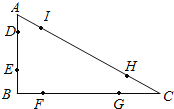根据题意，如图
，，
则的周长为12，
由图分析可得，距离三角形的三个顶点的距离均超过1的部分为线段上，
即其长度为6；
则蚂蚁距离三角形的三个顶点的距离均超过1的概率蚂蚁在三角形的边上爬行,其测度是长度,所求概率P(A)=
=.
(2)蚂蚁在三角形所在区域内部爬行,其测度是面积, 三角形的面积为
，
离三个顶点距离都不大于1的地方的面积为
，
所以其恰在离三个顶点距离都大于1的地方的概率为所求概率P(A)=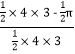
=1-
.
每日10分钟口算心算速算天天练系列答案科目：高中数学 来源： 题型：
【题目】如图，一个圆锥的底面半径为1，高为3，在圆锥中有一个半径为x的内接圆柱.
(1)试用x表示圆柱的高；
(2)当x为何值时，圆柱的侧面积最大，最大侧面积是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着资本市场的强势进入，互联网共享单车“忽如一夜春风来”，遍布了各个城市的大街小巷．为了解共享单车在
市的使用情况，某调研机构在该市随机抽取了
位市民进行调查，得到的
列联表如下：
经常使用 | 偶尔或不用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
（1）根据以上数据，能否在犯错误的概率不超过
的前提下认为使用共享单车的情况与年龄有关？
（2）现从所抽取的
岁以上的市民中利用分层抽样的方法再抽取
位市民，从这位市民中随机选出
位市民赠送礼品，求选出的位市民中至少有
位市民经常使用共享单车的概率．
参考公式及数据：
，
．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法正确的是 ． （写出所有正确说法的序号）
①若p是q的充分不必要条件，则p是q的必要不充分条件；
②命题“x∈R，x2+1＞3x”的否定是“x∈R，x2+1＜3x”；
③设x，y∈R．命题“若xy=0，则x2+y2=0”的否命题是真命题；
④若 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}满足an=2an﹣1+2n+1（n∈N* ， n≥2），a3=27．
（1）求a1 ， a2的值；
（2）是否存在一个实数t，使得bn= 
（an+t）（n∈N*），且数列{bn}为等差数列？若存在，求出实数t；若不存在，请说明理由；
（3）求数列{an}的前n项和Sn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，直四棱柱ABCD﹣A1B1C1D1底面是边长为1的正方形，高AA1= 
，点A是平面α内的一个定点，AA1与α所成角为 
，点C1在平面α内的射影为P，当四棱柱ABCD﹣A1B1C1D1按要求运动时（允许四棱柱上的点在平面α的同侧或异侧），点P所经过的区域的面积= ． 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的各项都大于1，且a1=2，a 
﹣an+1﹣a 
+1=0（n∈N*）．
（1）求证： 
≤an＜an+1≤n+2；
（2）求证： 
+ 
+ 
+…+ 
＜1．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的各项都大于1，且a1=2，a 
﹣an+1﹣a 
+1=0（n∈N*）．
（1）求证： 
≤an＜an+1≤n+2；
（2）求证： 
+ 
+ 
+…+ 
＜1．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a∈R，命题p：x∈[－2，－1]，x2－a≥0，命题q：
．
（1）若命题p为真命题，求实数a的取值范围；
（2）若命题“p∨q”为真命题，命题“p∧q”为假命题，求实数a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
